Discussion of the Dispersion Relation
The dispersion relation \(\boxed{m^2(z) \equiv \frac{(k^2 + l^2)(N^2(z) - \omega^2)}{\omega^2 - f^2}}\) with $l = 0$ can be written
$$
\omega^2 - f^2 = \frac{k^2}{m^2} \left( N^2 - \omega^2 \right)
$$
Introducing $\tan \theta = m / k$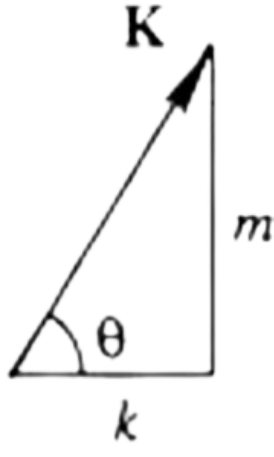 
$$
\omega^2 = f^2 \sin^2 \theta + N^2 \cos^2 \theta
$$
$$
\omega^2 = f^2 \sin^2 \theta + N^2 \cos^2 \theta
$$
$\omega$ is a function of the angle made by the wave number with the horizontal and is not a function of the magnitude of \(\mathbf{K}\). For $f = 0$, the aforementioned expression reduces to $\omega = N \cos \theta$
◀ ▶