Potential Vorticity Conservation in Shallow-Water Theory
Overall depth of the flow
\[h(x, y, t) = \underbrace{H}_{\text{mean depth}} + \underbrace{\eta(x,y,t)}_{\text{sea surface height}}\]
Zonal Momentum Equation
\[\underbrace{\frac{\partial u}{\partial t}}_{\text{local acceleration}}
+ \overbrace{u \frac{\partial u}{\partial x}}^{\text{nonlinear advection}}
+ \overbrace{v \frac{\partial u}{\partial y}}^{\text{nonlinear advection}}
- \underbrace{f v}_{\text{Coriolis (with } f = f_0 + \beta y \text{)}}
= -\underbrace{g \frac{\partial \eta}{\partial x}}_{\text{pressure gradient force from } \eta(x,y,t)}\]
Meridional Momentum Equation
\[\underbrace{\frac{\partial v}{\partial t}}_{\text{local acceleration}}
+ \overbrace{u \frac{\partial v}{\partial x}}^{\text{nonlinear advection}}
+ \overbrace{v \frac{\partial v}{\partial y}}^{\text{nonlinear advection}}
+ \underbrace{f u}_{\text{Coriolis (with } f = f_0 + \beta y \text{)}}
= -\underbrace{g \frac{\partial \eta}{\partial y}}_{\text{pressure gradient force from } \eta(x,y,t)}\]
Continuity Equation
\[\underbrace{\frac{\partial h}{\partial t}}_{\text{rate of change of depth}}
+ \underbrace{\frac{\partial (u h)}{\partial x}}_{\text{zonal transport divergence}}
+ \underbrace{\frac{\partial (v h)}{\partial y}}_{\text{meridional transport divergence}}
= 0\] Here, all the \(\overbrace{\text{nonlinear terms}}^{u \partial u/\partial x, \, v \partial u/\partial y, \ldots}\) have been retained
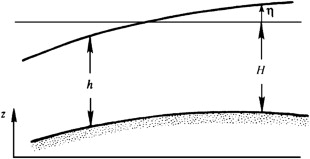
Shallow layer of instantaneous depth \(h(x,y,t)\) when the ocean bottom is not flat. \(\eta(x,y,t)\) is the height of the sea surface measured from a convenient horizontal reference plane. The x-axis is taken eastward; the y-axis is taken northward; \(u\) and \(v\) are the corresponding velocity components; and the Coriolis frequency is \( f = \underbrace{f_0}_{\text{reference}} + \underbrace{\beta y}_{\text{latitude dependent term}} \)