- Vortex lines move with the fluid
- The strength of a vortex tube (its circulation) is constant along its length
- A vortex tube cannot end within the fluid. It must either end at a boundary or form a closed loop – a vortex ring or loop
- The strength of a vortex tube remains constant in time
Regarding the total flux of vortex-lines passing through a material closed curve 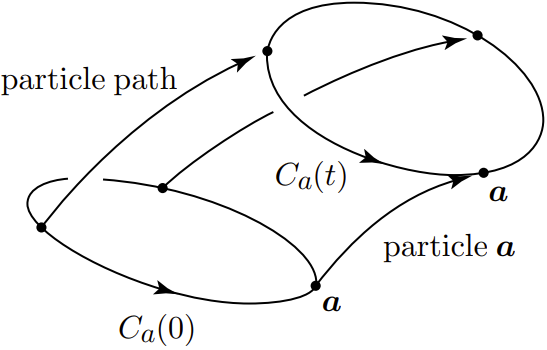 , Kelvin’s circulation theorem states that it is invariant with time for the motion of an ideal fluid of homentropy (subject to a conservative external force).
This is valid for flows of compressible fluids.
, Kelvin’s circulation theorem states that it is invariant with time for the motion of an ideal fluid of homentropy (subject to a conservative external force).
This is valid for flows of compressible fluids.
Here, we only highlight the proof of the first theorem, which essentially says that fluid particles that at any time are part of a vortex line always belong to the same vortex line.
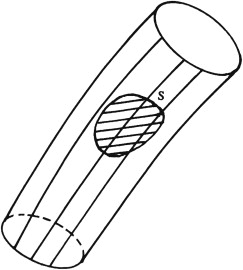
Consider an area S, bounded by a curve, lying on the surface of a vortex tube without embracing it.
Since the vorticity vectors are everywhere lying parallel to S (none are normal to S), it follows that the circulation around the edge of S is zero. After an interval of time, the same fluid particles form a new surface, S′.
According to Kelvin’s theorem, the circulation around S′ must also be zero. As this is true for any S, the component of vorticity normal to every element of S′ must vanish,
demonstrating that S′ must lie on the surface of the vortex tube.
Thus, vortex tubes move with the fluid, a result we will also be able to attain from the field equation for vorticity.
1 Tsutomu Kambe. (2007). Elementary Fluid Mechanics. World Scientific, Singapore.