Kelvin’s theorem can be proved by time differentiating the definition of the circulation \(\Gamma \equiv \oint_C \mathbf{u} \cdot d\mathbf{s} = \int_A \boldsymbol{\omega} \cdot \mathbf{n} \, dA\):

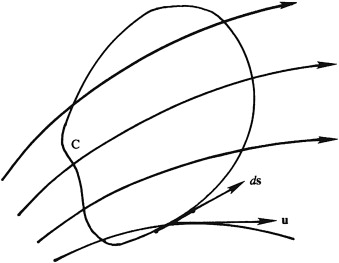
\[\frac{D\Gamma}{Dt} = \frac{D}{Dt} \oint_C u_i \, dx_i = \oint_C \frac{Du_i}{Dt} \, dx_i + \oint_C u_i \frac{D}{Dt} (dx_i)\] where \(dx_i\) are the components of the vector arc length element \(d\mathbf{x}\) of \(C\)

The first term on the right side may be rewritten: $$ \oint_C \frac{Du_i}{Dt} \, dx_i = \oint_C \left( -\frac{1}{\rho} \frac{\partial p}{\partial x_i} + g_i + \frac{1}{\rho} \frac{\partial \tau_{ij}}{\partial x_j} \right) dx_i = -\frac{1}{\rho} \oint_C dp - \oint_C d\Phi + \oint_C \left( \frac{1}{\rho} \frac{\partial \tau_{ij}}{\partial x_j} \right) dx_i $$ where the replacements \((\partial p / \partial x_i) dx_i = dp\) and \((\partial \Phi / \partial x_i) dx_i = d\Phi\) have been made, and \(\Phi\) is the body force potential of conservative body forces.
Body forces may be conservative or nonconservative. conservative body forces are those that can be expressed as the gradient of a potential function \(\boxed{ \mathbf{g} = - \nabla \Phi \quad \text{or} \quad g_j = -\frac{\partial \Phi}{\partial x_j}} \) where \(\Phi\) is called the force potential; it has units of energy per unit mass.