Kelvin introduced the idea of circulation and proved the following theorem: In an inviscid, barotropic flow with conservative body forces, the circulation around a closed curve moving with the fluid remains constant with time, if the motion is observed from a nonrotating frame. Kelvin's theorem is considered first and can be stated mathematically as $$ \frac{D\Gamma}{Dt} = 0 $$

$\frac{D}{Dt}$ is defined by Eulerian description of fluid motion $\boxed{\frac{DF}{Dt} \equiv \frac{\partial F}{\partial t} + \mathbf{u} \cdot \nabla F, \text{ or } \frac{DF}{Dt} \equiv \frac{\partial F}{\partial t} + u_i \frac{\partial F}{\partial x_i}}$ and represents the total time rate of change following the fluid elements that define the closed curve.
The scalar product $\mathbf{u} \cdot \nabla F$ is the magnitude of $\mathbf{u}$ times the component of $\nabla F$ in the direction of $\mathbf{u}$.
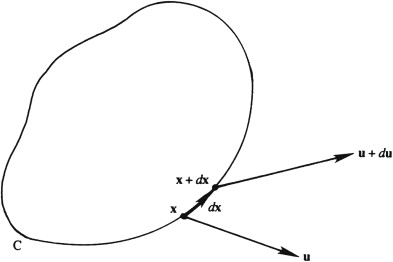
$C$ (a material contour) is used to compute the circulation $\Gamma$. Here the short segment $d\mathbf{x}$ of the contour $C$ moves with the fluid so that $D(d\mathbf{x})/Dt = d\mathbf{u}$.