For steady solid-body rotation, with a velocity field given by \(u_r = 0\) and \(u_\theta = \omega r/2\), the Euler equation in cylindrical coordinates simplifies to \( -\rho u_\theta^2 / r = -\frac{\partial p}{\partial r}, \quad 0 = -\frac{\partial p}{\partial z} - \rho g \)
Integrating these yields \( p(r,z) = \rho \frac{\omega^2 r^2}{8} + f(z) \Rightarrow p(r,z) = -\rho g z + g(r) \)
These two are consistent when \( p(r,z) - p_0 = \frac{1}{8} \rho \omega^2 r^2 - \rho g z \) where \(p_0\) is the pressure at \(r=0, z=0\)
Solving for \(z\) gives \( z = \frac{\omega^2 r^2}{8g} - \frac{p(r,z) - p_0}{\rho g} \)
Hence, surfaces of constant pressure in solid-body rotation are paraboloids of revolution

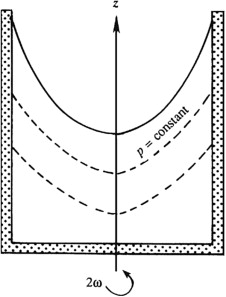
The Bernoulli function \( B = \frac{u^2}{2} + gz + \frac{p}{\rho} \) is not constant across different streamlines in rotational flow.
For an irrotational vortex (e.g., \(u_\theta = \Gamma/(2\pi r)\)), the viscous stress is \( \tau_{r\theta} = \mu \left[ \frac{1}{r} \frac{\partial u_r}{\partial \theta} + r \frac{\partial}{\partial r}\left(\frac{u_\theta}{r}\right) \right] = -\frac{\mu \Gamma}{\pi r^2}\), which is nonzero everywhere because fluid elements deform.
However, the net viscous force on an element at \(r > 0\) is zero because viscous forces on opposite surfaces cancel. Momentum conservation is still represented by Euler's equation. Substituting the vortex velocity into the radial Euler balance gives \( p(r,z) - p_\infty = -\frac{\rho \Gamma^2}{8 \pi^2 r^2} - \rho g z\) where \(p_\infty\) is the pressure far from the vortex line at \(z=0\)
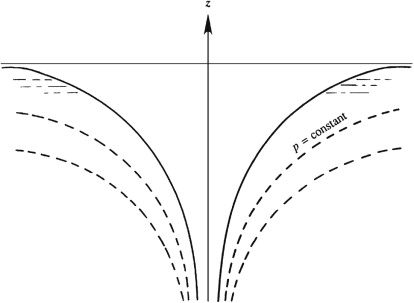
Rewriting \( z = -\frac{\Gamma^2}{8 \pi^2 r^2 g} - \frac{p(r,z) - p_\infty}{\rho g}. \) These surfaces of constant pressure are hyperboloids of revolution of the second degree