$$ H := \frac{u^2}{2} + h + \chi = \text{const.} \quad \text{along a stream-line} $$ This is called the Bernoulli theorem. The function $H$ is constant along a stream-line. Its value may be different for different stream-lines.

The Bernoulli equation is often applied to such a case where the fluid density is a constant everywhere, denoted by $\rho_0$, and $\chi = gz$ ($g$ is the constant gravity acceleration). Then the Bernoulli theorem can be written as $$ \rho_0 H = \rho_0 \frac{u^2}{2} + p + \rho_0 gz = \text{const.} $$ where $h = p/\rho_0 + e$ is used, and the internal energy $e$ is included in the “const.” on the right since $e$ is constant in a fluid of constant density and constant entropy

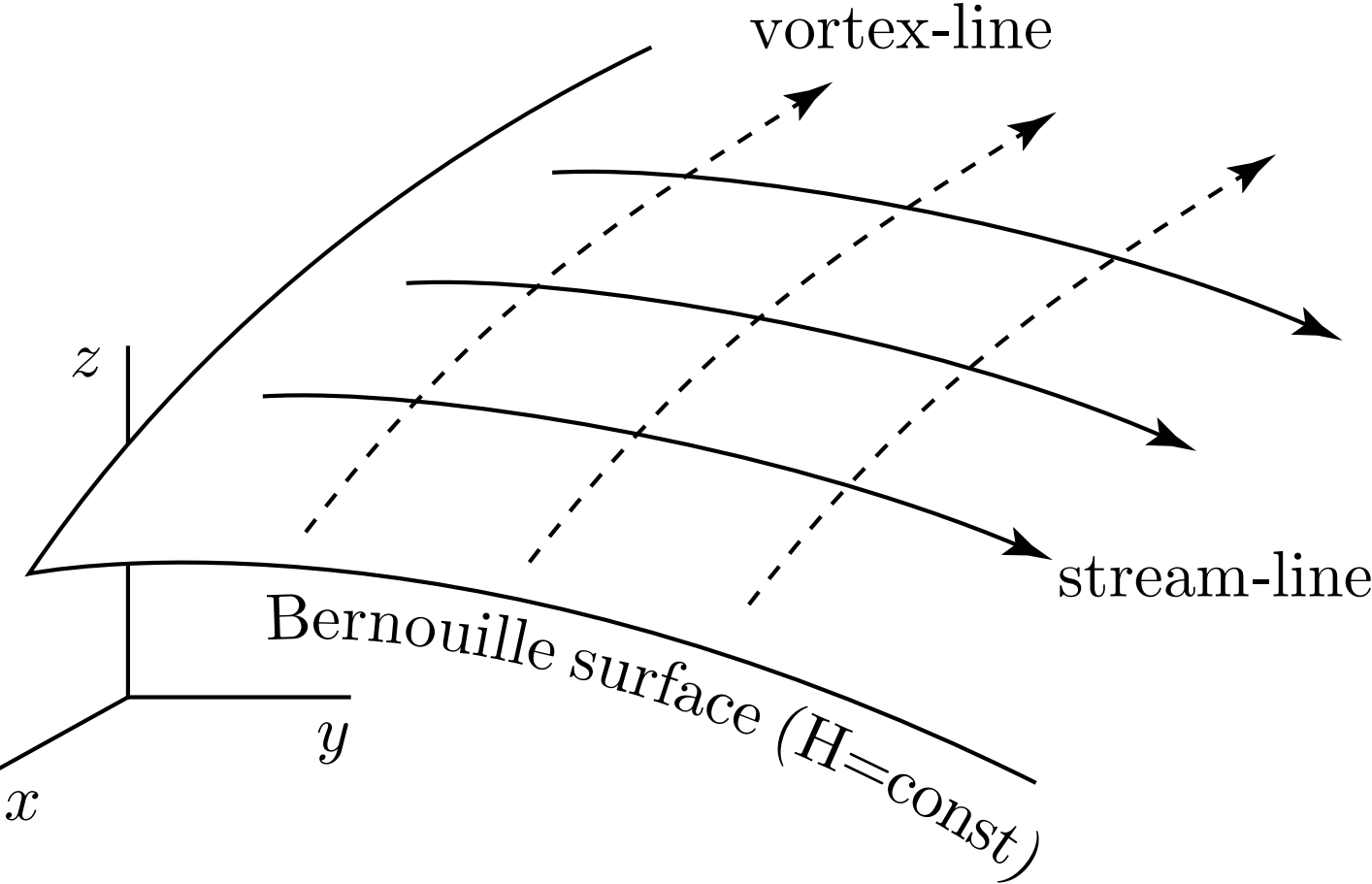
The inner product of $\boldsymbol{\omega}$ and $\boldsymbol{\omega} \times \mathbf{v}$ vanishes as well, the function $H$ is constant along a vortex-line analogously. A vortex-line is defined by $ dx / \omega_x = dy / \omega_y = dz / \omega_z $ where $\boldsymbol{\omega} = (\omega_x, \omega_y, \omega_z)$.

This implies that the surface given by $H(x, y, z) = \text{const.}$ is covered with a family of stream-lines and the vortex-lines crossing with the stream-lines.

In most flows, they are not parallel. The surface defined by $H = \text{const.}$ is called the Bernoulli surface

¹ Tsutomu Kambe. (2007). Elementary Fluid Mechanics. World Scientific, Singapore.