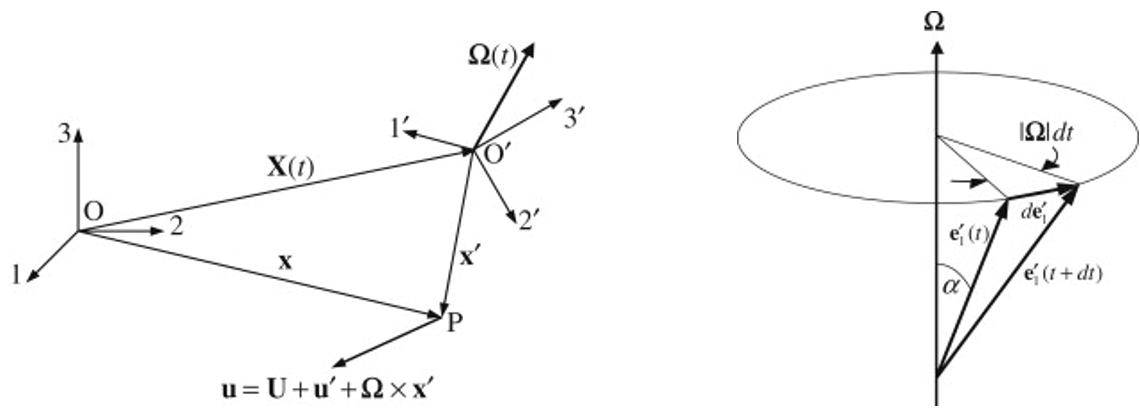
The velocity \( \mathbf{u} \) of the fluid particle is obtained by time differentiation:
\[ \mathbf{u} = \frac{d\mathbf{x}}{dt} = \frac{d\mathbf{X}}{dt} + \frac{d\mathbf{x'}}{dt} = \mathbf{U} + \frac{d}{dt} \left( x'_1 \mathbf{e}'_1 + x'_2 \mathbf{e}'_2 + x'_3 \mathbf{e}'_3 \right) \] \[ = \mathbf{U} + \underbrace{\frac{dx'_1}{dt} \mathbf{e}'_1 + \frac{dx'_2}{dt} \mathbf{e}'_2 + \frac{dx'_3}{dt} \mathbf{e}'_3}_{\mathbf{u'} \text{ (Velocity in rotating frame)}} + \underbrace{x'_1 \frac{d\mathbf{e}'_1}{dt} + x'_2 \frac{d\mathbf{e}'_2}{dt} + x'_3 \frac{d\mathbf{e}'_3}{dt}}_{\mathbf{\Omega} \times \mathbf{x'} \text{ (Rotational contribution)}} \] \[ = \mathbf{U} + \mathbf{u'} + \mathbf{\Omega} \times \mathbf{x'} \]The final equality is based on the geometric construction of the cross product for \( \mathbf{e}'_1 \), one of the unit vectors in the rotating frame. In a small time \( dt \), the rotation of \( O'1'2'3' \) causes \( \mathbf{e}'_1 \) to trace a small portion of a cone with radius \( \sin \alpha \) as shown. The magnitude of the change in \( \mathbf{e}'_1 \) is \( |\mathbf{e}'_1| = (\sin \alpha) |\boldsymbol{\Omega}| dt \), so \( d|\mathbf{e}'_1|/dt = (\sin \alpha) |\boldsymbol{\Omega}| \), which is equal to the magnitude of \( \boldsymbol{\Omega} \times \mathbf{e}'_1 \). The direction of the rate of change of \( \mathbf{e}'_1 \) is perpendicular to \( \boldsymbol{\Omega} \) and \( \mathbf{e}'_1 \), which is the direction of \( \boldsymbol{\Omega} \times \mathbf{e}'_1 \). Thus, by geometric construction, \( \frac{d \mathbf{e}'_1}{dt} = \boldsymbol{\Omega} \times \mathbf{e}'_1 \), and by direct extension to the other unit vectors, \( \frac{d \mathbf{e}'_i}{dt} = \boldsymbol{\Omega} \times \mathbf{e}'_i \).