Noninertial Frame of Reference

A frame of reference \( O'1'2'3' \) that translates at velocity \( \frac{d\mathbf{X}(t)}{dt} = \mathbf{U}(t) \) and rotates at angular velocity \( \mathbf{\Omega}(t) \) with respect to a stationary frame of reference \( O123 \). The vectors \( \mathbf{U} \) and \( \mathbf{\Omega} \) may be resolved in either frame. The same clock is used in both frames so \( t = t' \). A fluid particle \( P \) can be located in the rotating frame at \( \mathbf{x'} = (x'_1, x'_2, x'_3) \) or in the stationary frame at \( \mathbf{x} = (x_1, x_2, x_3) \), and these distances are simply related via vector addition: \(\mathbf{x} = \mathbf{X} + \mathbf{x'}\)

The velocity \( \mathbf{u} \) of the fluid particle is obtained by time differentiation:

\[ \mathbf{u} = \frac{d\mathbf{x}}{dt} = \frac{d\mathbf{X}}{dt} + \frac{d\mathbf{x'}}{dt} = \mathbf{U} + \frac{d}{dt} \left( x'_1 \mathbf{e}'_1 + x'_2 \mathbf{e}'_2 + x'_3 \mathbf{e}'_3 \right) \] \[ = \mathbf{U} + \underbrace{\frac{dx'_1}{dt} \mathbf{e}'_1 + \frac{dx'_2}{dt} \mathbf{e}'_2 + \frac{dx'_3}{dt} \mathbf{e}'_3}_{\mathbf{u'} \text{ (Velocity in rotating frame)}} + \underbrace{x'_1 \frac{d\mathbf{e}'_1}{dt} + x'_2 \frac{d\mathbf{e}'_2}{dt} + x'_3 \frac{d\mathbf{e}'_3}{dt}}_{\mathbf{\Omega} \times \mathbf{x'} \text{ (Rotational contribution)}} \] \[ = \mathbf{U} + \mathbf{u'} + \mathbf{\Omega} \times \mathbf{x'} \]
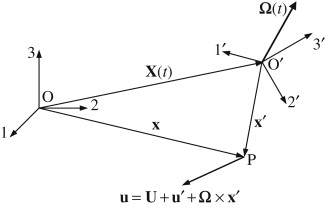
CoordinateSystemO

Geometry showing the relationship between a stationary coordinate system \( O123 \) and a noninertial coordinate system \( O'1'2'3' \) that is moving, accelerating, and rotating with respect to \( O123 \)

In particular, the vector connecting \( O \) and \( O' \) is \( \mathbf{X}(t) \) and the rotational velocity of \( O'1'2'3' \) is \( \mathbf{\Omega}(t) \). The vector velocity \( \mathbf{u} \) at point \( P \) in \( O123 \) is shown. The vector velocity \( \mathbf{u'} \) at point \( P \) in \( O'1'2'3' \) differs from \( \mathbf{u} \) because of the motion of \( O'1'2'3' \)

◀ ▶