At any fixed position, the rate of change of the phase with time is \( \frac{\partial \theta}{\partial t} = -\omega \) where \( \omega \) is the rate of decrease of phase, as wave crests move, the phase decreases at a fixed location

How long do we have to wait until the same phase appears? The wave period \( T \) is the shortest time for the same phase to reappear defined by \( \omega T = 2\pi \Rightarrow T = \frac{2\pi}{\omega} \)
What is the speed of movement of the line of constant phase? \( \theta = k_j x_j - \omega t = Ks - \omega t \) As \(t\) increases, \(s\) must increase to keep the phase constant 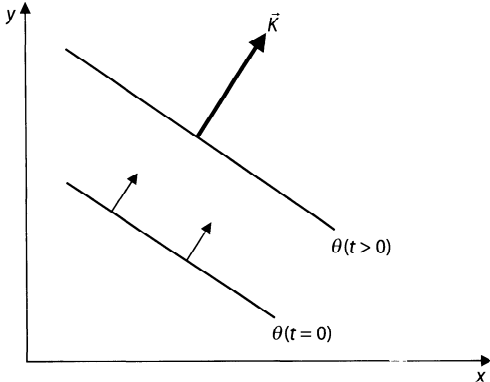\( \left( \frac{\partial s}{\partial t} \right)_{\theta} = -\frac{\partial \theta / \partial t}{\partial \theta / \partial s} = \frac{\omega}{K} \) The appearance of the minus sign is because at constant \(\theta\), \(\delta \theta = 0 = K ds - \omega dt\), so that \(ds/dt = \omega/K\)

In 2D the phase speed in the \(x\)-direction would be defined, at fixed \(y\), \( d\theta = 0 = k dx - \omega dt \text{ or } c_x = \frac{\omega}{k} = -\frac{\partial \theta / \partial t}{\partial \theta / \partial x} \) Also, the increase in phase along the wave vector is \( \Delta \theta = \int \frac{\partial \theta}{\partial s} ds = \int K ds \)
In all physical wave problems, the dynamics will impose a relation between the wave vector and the frequency. This relation is called the dispersion relation. The form of the dispersion relation can be written as \[ \omega = \Omega(k_j) \]