The function \( \phi \) we have considered above is constant on the surface where \( \theta \) is constant, i.e., \( k_i x_i - \omega t = \text{constant} \)
In two dimensions these are the lines \( \vec{K} \cdot \vec{x} - \omega t = k_1 x_1 + k_2 x_2 - \omega t \equiv kx + ly - \omega t \) (\( k_1 = k, k_2 = l, k_3 = m \) in Cartesian coordinates)

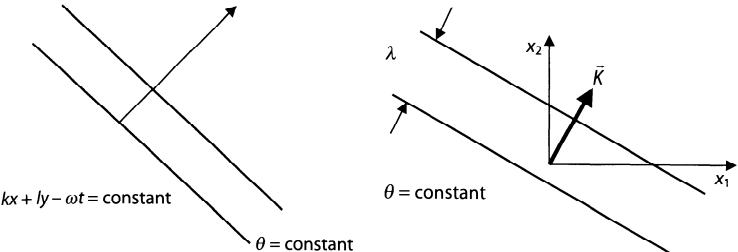
The directions of the lines of constant phase are given by the normal to those lines of constant \( \theta \) \[ \nabla \theta = \nabla (\vec{K} \cdot \vec{x} - \omega t) = \vec{K} \] or equivalently \[ \frac{\partial \theta}{\partial x_i} = \frac{\partial}{\partial x_i} (k_j x_j - \omega t) = k_j \frac{\partial x_j}{\partial x_i} = k_j \delta_{ij} = k_i \]

Define \(K = |\vec{K}|\) (the magnitude of the wave vector) \(\Rightarrow \boxed{\vec{K} \cdot \vec{x} = Ks}\) where \( s \) is the scalar distance perpendicular to the line of constant phase (e.g., where \( \phi \) reaches a maximum)
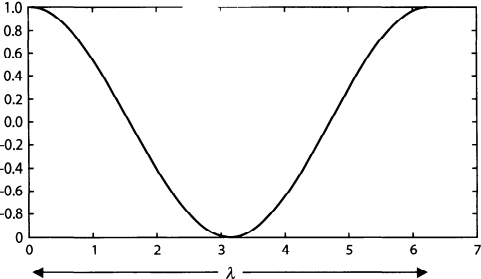
The plane wave is a spatially periodic function, so \( \phi(Ks) = \phi(K[s+\lambda]) \) where \( K \lambda = 2\pi \)

Because \( e^{i(Ks)} = e^{i(Ks + 2\pi)}, \quad e^{i(2\pi)} \equiv 1 \)

The wavelength \( \lambda \) is \( \lambda = \frac{2\pi}{K} \), it is the distance along the wave vector between two points of the same phase