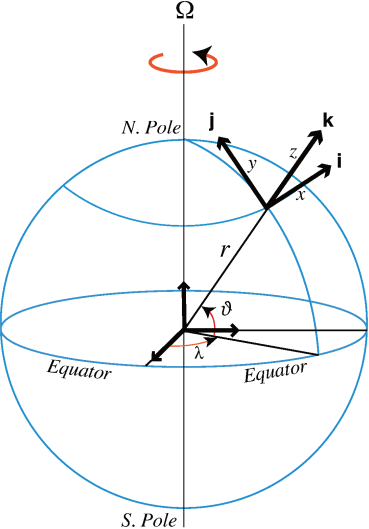
The location of a point is given by the coordinates \((\lambda, \vartheta, r)\)
• \( \lambda \) is the angular distance eastwards (longitude)
• \( \vartheta \) is the angular distance polewards (latitude)
• \( r \) is the radial distance from the center of the Earth
If \( a \) is the Earth's radius, then \[ z = r - a \] At a given location, the Cartesian increments \((\delta x, \delta y, \delta z)\) are \[ (\delta x, \delta y, \delta z) = (r \cos \vartheta \, \delta \lambda, r \, \delta \vartheta, \delta r) \] For a scalar quantity \( \phi \), the material derivative in spherical coordinates is \[ \frac{D\phi}{Dt} = \frac{\partial \phi}{\partial t} + \frac{u}{r \cos \vartheta} \frac{\partial \phi}{\partial \lambda} + \frac{v}{r} \frac{\partial \phi}{\partial \vartheta} + w \frac{\partial \phi}{\partial r} \] where the velocity components corresponding to \((\lambda, \vartheta, r)\) are \[ (u, v, w) \equiv \left( r \cos \vartheta \frac{D\lambda}{Dt}, r \frac{D\vartheta}{Dt}, \frac{Dr}{Dt} \right) \]

\( u \) is the zonal velocity, \( v \) is the meridional velocity, \( w \) is the vertical velocity
Define \( (\mathbf{i}, \mathbf{j}, \mathbf{k}) \) to be the unit vectors in the direction of increasing \((\lambda, \vartheta, r)\), then \( \boxed{\mathbf{v} = i u + j v + k w} \) Also note that \( \frac{Dr}{Dt} = \frac{Dz}{Dt} \)