\(\epsilon = \frac{U}{2\Omega L}\) was small for large-scale flows. It is now apparent that for large-scale flows the applied forces produce primarily a Coriolis acceleration. The acceleration must be in the direction of the resultant of the force, so that the relative velocity required to produce the Coriolis acceleration must be directed to the right of the applied force

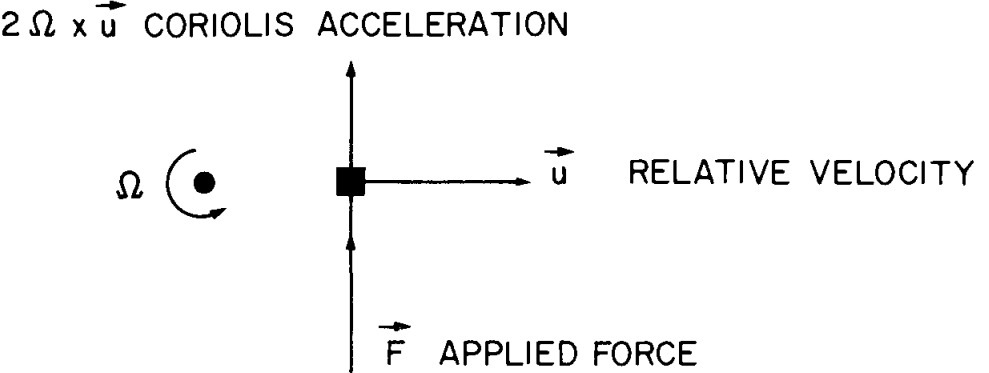
The Coriolis acceleration becomes dominant for large-scale flows, not because the Coriolis acceleration becomes large, but because the relative accelerations become so feeble when the scale of the motion is large. When the time scale of the motion exceeds the rotation period, the Coriolis acceleration exceeds the relative acceleration in importance

The rotational frequency of the Earth is given by \(\Omega = \frac{2\pi}{86400} \approx 7.27 \times 10^{-5} \text{s}^{-1}\), the length of the day is 86400 seconds

\( 2\Omega \times \mathbf{u} \cong (-2\Omega v \sin \theta, \, 2\Omega u \sin \theta, \, -2\Omega u \cos \theta) = (-fv, \, fu, \, -2\Omega u \cos \theta), \quad \text{where} \quad f = 2\Omega \sin \theta \)

The gyroscopic tendency of fluid elements to move at right angles to the applied force is in fact responsible for the unique character of geophysical fluid dynamics

¹ Pedlosky, J. (1982). Geophysical Fluid Dynamics. Springer study edition. Springer, Berlin, Heidelberg.