To obtain a description of the motion entirely in terms of quantities which are directly observed in the rotating frame, \( \mathbf{u}_I = \mathbf{u}_R + \boldsymbol{\Omega} \times \mathbf{r} \) is used to eliminate \( \mathbf{u}_I \) from the \( \left( \frac{d\mathbf{u}_I}{dt} \right)_I = \boxed{\left( \frac{d\mathbf{u}_I}{dt} \right)_R + \boldsymbol{\Omega} \times \mathbf{u}_I} \) \[ \left( \frac{d\mathbf{u}_I}{dt} \right)_I = \left( \frac{d\mathbf{u}_R}{dt} \right)_R + \frac{d\boldsymbol{\Omega}}{dt} \times \mathbf{r} + \boldsymbol{\Omega} \times \left( \frac{d\mathbf{r}}{dt} \right)_R + \boldsymbol{\Omega} \times (\mathbf{u}_R + \boldsymbol{\Omega} \times \mathbf{r})\\ = \left( \frac{d\mathbf{u}_R}{dt} \right)_R + 2\boldsymbol{\Omega} \times \mathbf{u}_R + \boldsymbol{\Omega} \times (\boldsymbol{\Omega} \times \mathbf{r}) + \frac{d\boldsymbol{\Omega}}{dt} \times \mathbf{r} \]

The discrepancy between the accelerations perceived in the different frames is equal to the three additional terms of \(\left( \frac{d\mathbf{u}_R}{dt} \right)_R + 2\boldsymbol{\Omega} \times \mathbf{u}_R + \boldsymbol{\Omega} \times (\boldsymbol{\Omega} \times \mathbf{r}) + \frac{d\boldsymbol{\Omega}}{dt} \times \mathbf{r}\)

The Coriolis acceleration: \( 2\boldsymbol{\Omega} \times \mathbf{u}_R \)
The centripetal acceleration: \( \boldsymbol{\Omega} \times (\boldsymbol{\Omega} \times \mathbf{r}) \)
The acceleration due to variation in rotation rate: \( \frac{d\boldsymbol{\Omega}}{dt} \times \mathbf{r} \) (usually negligible for most oceanographic or atmospheric phenomena, except when time scales are extremely long)

\( \boldsymbol{\Omega} \) can be considered constant. The centripetal term can be rewritten using \( \mathbf{r}_\perp \), the perpendicular distance from the rotation axis to the position vector \( \mathbf{r} \)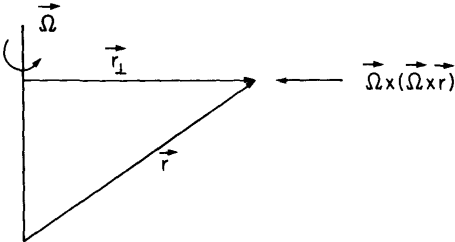 CentripetalAcceleration
\(\because \boldsymbol{\Omega} \times \mathbf{r} = \boldsymbol{\Omega} \times \mathbf{r}_\perp \)
\(\therefore\) Using the triple vector product identity \( \mathbf{A} \times (\mathbf{B} \times \mathbf{C}) = (\mathbf{A} \cdot \mathbf{C}) \mathbf{B} - (\mathbf{A} \cdot \mathbf{B}) \mathbf{C} \Rightarrow \boldsymbol{\Omega} \times (\boldsymbol{\Omega} \times \mathbf{r}) = -|\boldsymbol{\Omega}|^2 \mathbf{r}_\perp \)

¹ Pedlosky, J. (1982). Geophysical Fluid Dynamics. Springer study edition. Springer, Berlin, Heidelberg.