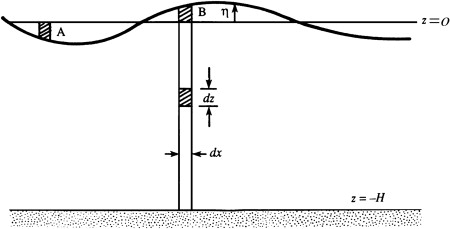
The potential energy per unit horizontal area, \( E_p \), of the wave system is defined as the work done per unit area to deform a horizontal free surface into the disturbed state.
It is therefore equal to the difference of potential energies of the system in the disturbed and undisturbed states. As the potential energy of an element in the fluid (per unit length in \( y \)) is \( \rho gz \, dx \, dz \)

\( E_p \) can be calculated as \[ E_p = \frac{\rho g}{\lambda} \int_0^\lambda \int_{-H}^\eta z \, dz \, dx - \frac{\rho g}{\lambda} \int_0^\lambda \int_{-H}^0 z \, dz \, dx = \frac{\rho g}{\lambda} \int_0^\lambda \int_0^\eta z \, dz \, dx = \frac{\rho g}{2\lambda} \int_0^\lambda \eta^2 \, dx, \]

Written in terms of the mean square displacement \[ E_p = \frac{1}{2} \rho g \overline{\eta^2} \]

Thus, the average kinetic and potential energies are equal. This is called the principle of equipartition of energy and is valid in conservative dynamical systems undergoing small oscillations that are unaffected by planetary rotation. However, it is not valid when the Coriolis acceleration is included. The total wave energy in the water column per unit horizontal area is \[ E = E_k + E_p = \rho g \overline{\eta^2} = \frac{1}{2} \rho g a^2 \] the last form in terms of the amplitude \( a \) is valid if \( \eta \) is assumed sinusoidal, since the average over a wavelength of the square of a sinusoid is 1/2

◀ ▶