Streamlines may be found from the stream function \(\psi\), which can be determined by integrating the velocity component equations \(\partial \psi / \partial z = u\) and \(-\partial \psi / \partial x = w\) when \(u\) and \(w\) are given by \(u = a\omega \frac{\cosh(k(z + H))}{\sinh(kH)} \cos(kx - \omega t)\) and \(w = a\omega \frac{\sinh(k(z + H))}{\sinh(kH)} \sin(kx - \omega t)\): \[ \psi = \frac{a \omega}{k} \frac{\sinh(k(z + H))}{\sinh(kH)} \cos(kx - \omega t) \]

To understand the streamline structure, consider a particular time \(t = 0\) when \[ \psi \propto \sinh[k(z + H)] \cos(kx) \] \(\psi = 0\) at \(z = -H\), so that the bottom wall is a part of the \(\psi = 0\) streamline, \(\psi\) is also zero at \(kx = \pm \pi/2, \pm 3\pi/2, \dots\) for any \(z\)
At \(t = 0\) and at these values of \(kx\), \(\eta\) from \(\eta(x,t) = a \cos[kx - \omega t]\) vanishes

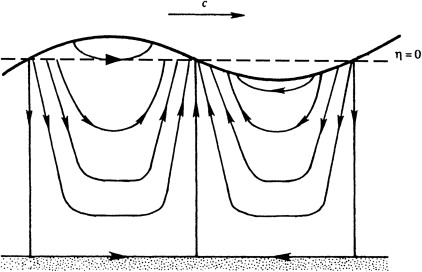
StreamlineSinusoidalSurfaceWavePropagating

The resulting streamline pattern is shown here for a sinusoidal surface wave propagating to the right, the velocity is in the direction of propagation (and horizontal) at all depths below the crests, and opposite to the direction of propagation at all depths below troughs. Here the \( \psi = 0 \) streamline follows the bottom and jumps up to contact the surface where \( \eta = 0 \). The remaining streamlines start and end on the liquid surface with purely horizontal motion found in the \( +x \) direction below a wave crest and in \( -x \) direction below a wave trough

◀ ▶