When the control volume is used with \( \mathbf{b} = \mathbf{u}_s \) and the integral form of the energy conservation equation accounting for internal and kinetic energy, work done by body and surface forces, and heat flux across a boundary\(\boxed{\small \frac{d}{dt} \int_{V^*(t)} \rho \left( e + \frac{1}{2} |\mathbf{u}|^2 \right) dV + \int_{A^*(t)} \left( \rho e + \frac{\rho}{2} |\mathbf{u}|^2 \right) (\mathbf{u} - \mathbf{b}) \cdot \mathbf{n} \, dA = \int_{V^*(t)} \rho \mathbf{g} \cdot \mathbf{u} \, dV + \int_{A^*(t)} \mathbf{f} \cdot \mathbf{u} \, dA - \int_{A^*(t)} \mathbf{q} \cdot \mathbf{n} \, dA} \)

the following energy-conservation boundary condition can be developed \[ \dot{m}_s \left[ \left( h + \frac{1}{2} |\mathbf{u}|^2 \right)_2 - \left( h + \frac{1}{2} |\mathbf{u}|^2 \right)_1 \right] = - (k \nabla T)_2 \cdot \mathbf{n} + (k \nabla T)_1 \cdot \mathbf{n} \] When \( \dot{m}_s = 0 \), the conductive heat flux must be continuous at the interface

For a complete set of boundary conditions, the thermal equivalent of the no-slip condition \[ T_1 = T_2 \] is needed on the interface, no temperature jump is permitted

However, it is known to be violated in rarefied gases and is related to viscous slip in such flows

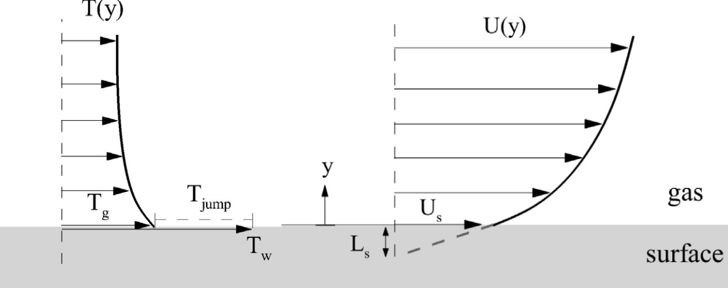
Velocity slip (\( U_s \)), slip length (\( L_s = \frac{U_s}{dU/dy} \)), and temperature jump (\( T_{\text{jump}} \)) in the presence of non-equilibrium gas–surface interactions in rarefied gas flows

¹ Hassan Akhlaghi, Ehsan Roohi and Stefan Stefanov. A Comprehensive Review on Micro- and Nano-Scale Gas Flow Effects: Slip-Jump Phenomena, Knudsen Paradox, Thermally-Driven Flows, and Knudsen Pumps. Physics Reports, vol. 997, 1 Jan. 2023, pp. 1–60.

◀ ▶