Return to the development of conservation of momentum boundary conditions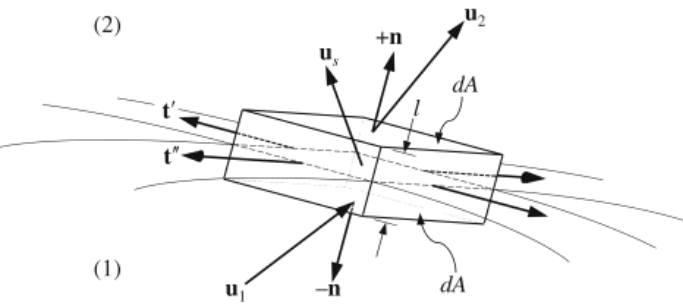 
and consider the normal direction. In this case, the momentum conservation result obtained from \(\boxed{\mathbf{g} = -\nabla \Phi \quad \text{or} \quad g_j = -\frac{\partial \Phi}{\partial x_j}}
\) and \(\boxed{\int_{A(t)} \mathbf{f}(\mathbf{n}, \mathbf{x}, t) \, dA
= \int_{A(t)} n_i T_{ij} \, dA
= \int_{V(t)} \frac{\partial}{\partial x_i}(T_{ij}) \, dV}\) with \( \mathbf{b} = \mathbf{u}_s \) is
\[
\dot{m}_s \, (\mathbf{u}_2 - \mathbf{u}_1) \cdot \mathbf{n} = - (p_2 - p_1) + \left( (n_i \tau_{ij})_2 - (n_i \tau_{ij})_1 \right) n_j + \sigma \left( \frac{1}{R'} + \frac{1}{R''} \right)
\]
\( \tau_{ij} \) is the viscous stress tensor given by conservation of energy \(\tau_{ij} = \mu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right)
+ \left( \mu_v - \frac{2}{3} \mu \right) \frac{\partial u_m}{\partial x_m} \delta_{ij}\), and the tangent unit vectors \( \mathbf{t}' \) and \( \mathbf{t}'' \) lie along the principal directions of interface curvature (with radii of curvature \( R' \) and \( R'' \))
When both fluids are not moving, or when \( \dot{m}_s = 0 \) and the fluids are inviscid, this equation reduces to pressure difference across the interface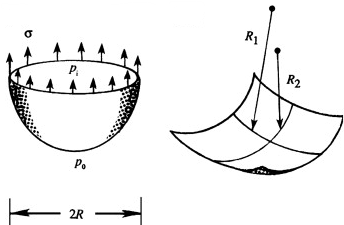 
\(p_i - p_o = \sigma \left( \frac{1}{R_1} + \frac{1}{R_2} \right)
\)