The equations representing conservation of mass in a flowing fluid are based on the principle that the mass of a specific collection of neighboring fluid particles is constant. The volume occupied by a specific collection of fluid particles is called a material volume \(V(t)\)
Such a volume moves and deforms within a fluid flow so that it always contains the same mass elements; none enter the volume and none leave it. This implies that a material volume’s surface \( A(t) \), a material surface, must move at the local fluid velocity \( \mathbf{u} \) so that fluid particles inside \( V(t) \) remain inside and fluid particles outside \( V(t) \) remain outside
Conservation of mass for a material volume in a flowing fluid, \( \rho \) is the fluid density: \[ \frac{d}{dt} \int_{V(t)} \rho(\mathbf{x}, t) \, dV = 0 \]
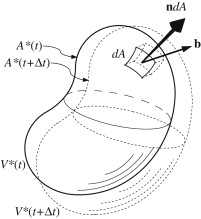
The primary concept here is equivalent to an infinitely flexible, perfectly sealed thin-walled balloon containing fluid. The balloon’s contents play the role of the material volume \( V(t) \) with the balloon itself defining the material surface \( A(t) \). Because the balloon is sealed, the total mass of fluid inside the balloon remains constant as the balloon moves, expands, contracts, or deforms