From Leibniz's Theorem to the Reynolds Transport Theorem
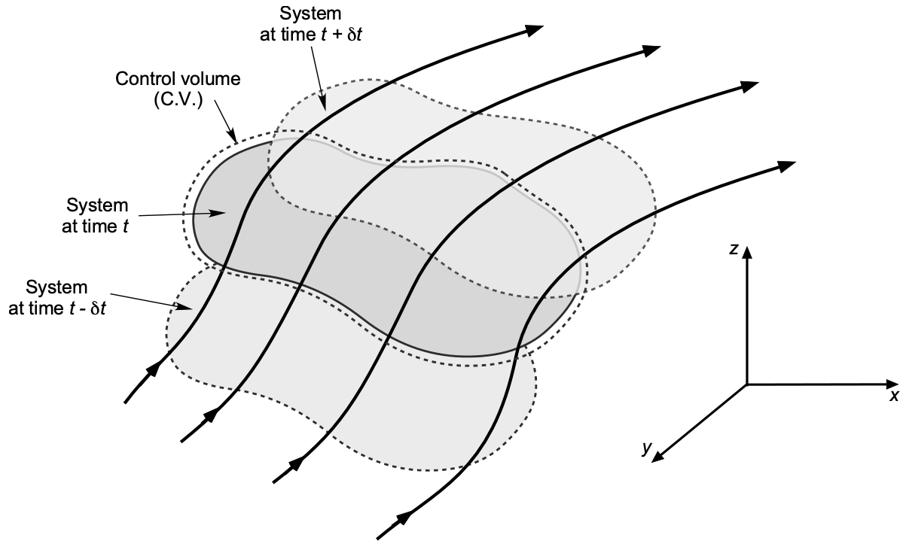
1Professor John M. Cimbala. ME 320 Fluid Flow.
2Introduction to Aerospace Flight Vehicles.
https://eaglepubs.erau.edu/introductiontoaerospaceflightvehicles/chapter/equations-of-fluid-motion/