Consider a function \( F \) that depends on one independent spatial variable, \( x \), and time \( t \). In addition assume that the time derivative of its integral is of interest when the limits of integration, \( a \) and \( b \), are themselves functions of time. Leibniz's theorem states the time derivative of the integral of \( F(x,t) \) between \( x = a(t) \) and \( x = b(t) \) is \[ \frac{d}{dt} \int_{x = a(t)}^{x = b(t)} F(x,t)\, dx = \int_{a}^{b} \frac{\partial F}{\partial t} \, dx + \frac{db}{dt} F(b,t) - \frac{da}{dt} F(a,t) \] where \( a \), \( b \), \( F \), and their derivatives appearing on the right side are all evaluated at time \( t \)
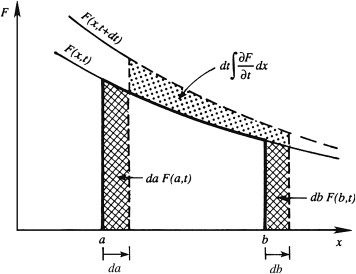
Graphical illustration of the Leibniz theorem. The three marked areas correspond to the three contributions shown on the right in \(
\frac{d}{dt} \int_{x = a(t)}^{x = b(t)} F(x,t)\, dx = \boxed{\int_{a}^{b} \frac{\partial F}{\partial t} \, dx + \frac{db}{dt} F(b,t) - \frac{da}{dt} F(a,t)}
\) The continuous line shows the integral \( \int F dx \) at time \( t \), and the dashed line shows the integral at time \( t + dt \)
The first term on the right side is the integral of \( \partial F/\partial t \) between \( x = a \) and \( b \), the second term is the gain of \( F \) at the upper limit which is moving at rate \( db/dt \),
and the third term is the loss of \( F \) at the lower limit which is moving at rate \( da/dt \)
The essential features are the total time derivative on the left, an integral over the partial time derivative of the integrand on the right, and terms that account for the time-dependence of the limits of integration on the right
These features persist when \(\frac{d}{dt} \int_{x = a(t)}^{x = b(t)} F(x,t)\, dx = \int_{a}^{b} \frac{\partial F}{\partial t} \, dx + \frac{db}{dt} F(b,t) - \frac{da}{dt} F(a,t)\) is generalized to three dimensions