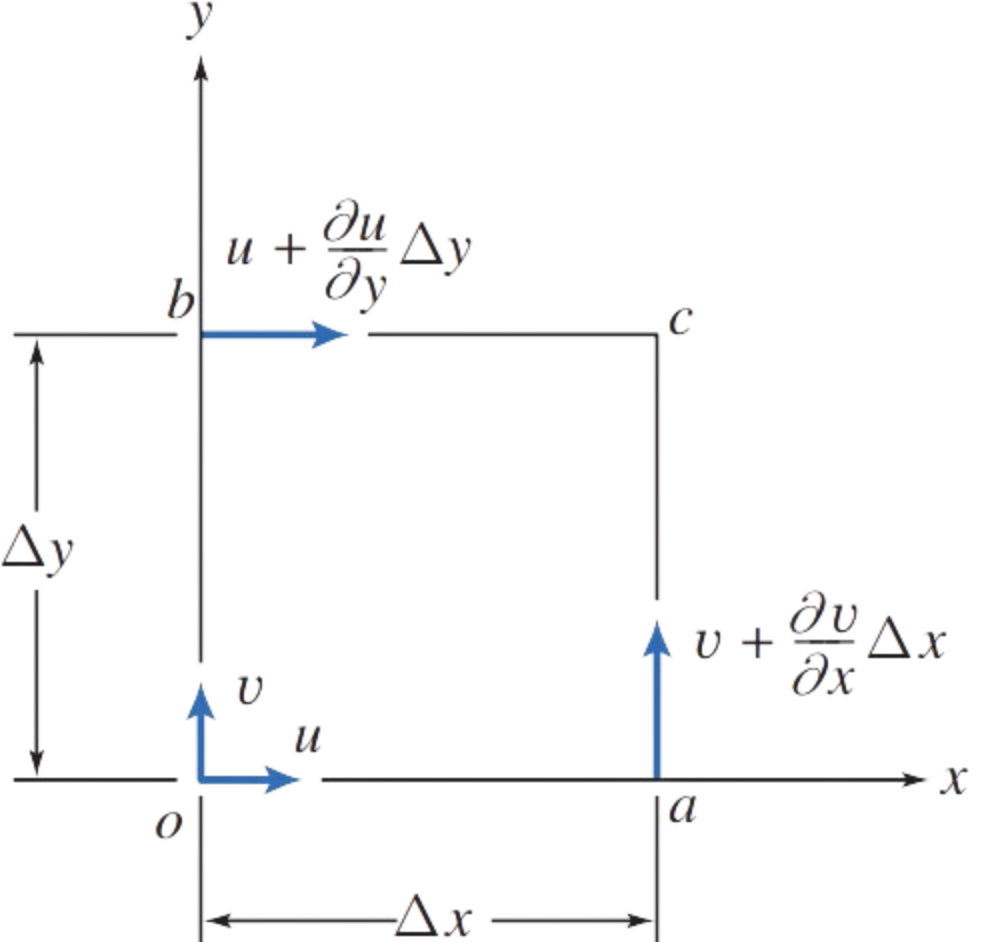
We can develop a relationship between circulation and vorticity by considering the rectangular circuit, where the velocity components at \( o \) are assumed to be \( (u, v) \), and the velocities along segments \( bc \) and \( ac \) can be derived using Taylor series approximations
For the closed curve \( oacb \) 
\(
\Delta \Gamma = u \Delta x + \left( v + \frac{\partial v}{\partial x} \Delta x \right) \Delta y - \left( u + \frac{\partial u}{\partial y} \right) \Delta x - v \Delta y
\)
\(
\Delta \Gamma = \left( \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} \right) \Delta x \Delta y
\)
\(
\Delta \Gamma = 2 \omega_z \Delta x \Delta y
\)
Then \[ \Gamma = \oint_{c} \vec{V} \cdot d\vec{s} = \int_{A} 2 \omega_z \, dA = \int_{A} \left( \nabla \times \vec{V} \right)_z dA \]
Equation above is a statement of the Stokes Theorem in two dimensions. Thus, the circulation around a closed contour is equal to the total vorticity enclosed within it
1Fox and McDonald's Introduction to Fluid Mechanics, 8th Edition.