Fluid Rotation

The factor of \( \frac{1}{2} \) can be eliminated from \(\boxed{\vec{\omega} = \frac{1}{2} \nabla \times \vec{V}}\) by defining the vorticity, \( \zeta \), to be twice the rotation, \[ \zeta = 2\vec{\omega} = \nabla \times \vec{V} \] The vorticity is a measure of the rotation of a fluid element as it moves in the flow field

The circulation \( \Gamma \), is defined as the line integral of the tangential velocity component about any closed curve fixed in the flow \[ \Gamma = \oint_{c} \vec{V} \cdot d\vec{s} \] where \( d\vec{s} \) is an elemental vector tangent to the curve and having length \( ds \) of the element of arc; a positive sense corresponds to a counterclockwise path of integration around the curve

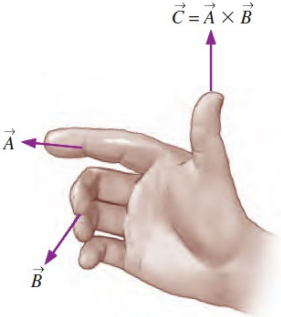
  • The vorticity vector is defined as the curl of the velocity vector, using the right-hand rule \( \vec{\zeta} = \nabla \times \vec{V} \)
  • It turns out that vorticity is equal to twice the angular velocity of a fluid particle \( \vec{\zeta} = 2\vec{\omega} \)
  • Thus, vorticity is a measure of rotation of a fluid particle
    • if \( \vec{\zeta} = 0 \), the flow is irrotational
    • if \( \vec{\zeta} \neq 0 \), the flow is rotational
VorticityRightHandRule

1John M. Cimbala. ME 320 Fluid Flow.

◀ ▶