Consider the xy plane view of the particle at time t
- The left and lower sides of the particle are given by the two perpendicular line segments oa and ob of lengths Δx and Δy in (a)
- In general, after an interval Δt the particle will have translated to some new position, and also have rotated and deformed. A possible instantaneous orientation of the lines at time t + Δt is shown in (b)
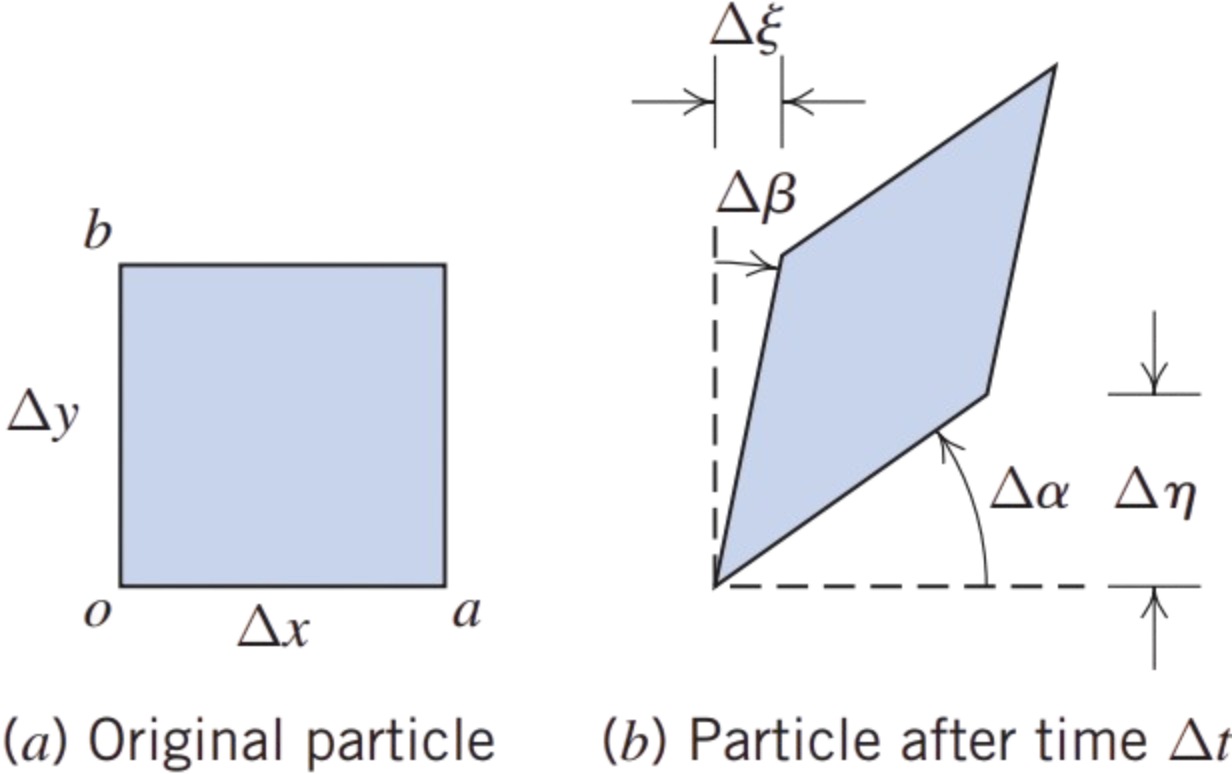
We need to be careful here with our signs for angles. Following the right-hand rule, counterclockwise rotation is positive, and we have shown side \( oa \) rotating counterclockwise through angle \( \Delta \alpha \), but
be aware that we have shown edge \( ob \) rotating at a clockwise angle \( \Delta \beta \).
Both angles are obviously arbitrary, but it will help visualize the discussion if we assign values to these angles, e.g., let \( \Delta \alpha = 6^\circ \) and \( \Delta \beta = -4^\circ \).
How do we extract from \( \Delta \alpha \) and \( \Delta \beta \) a measure of the particle’s rotation?
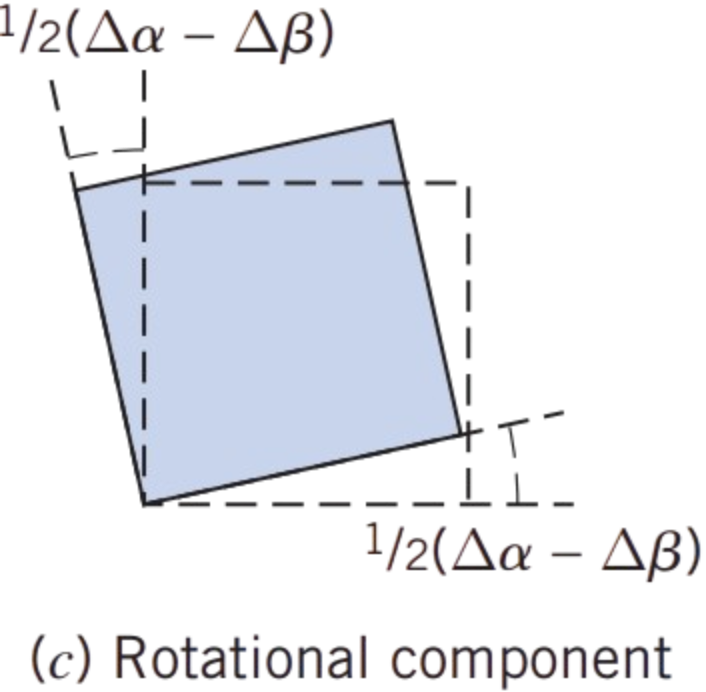
The answer is that we take an average of the rotations \( \Delta \alpha \) and \( \Delta \beta \), so that the particle’s rigid body counterclockwise rotation is
\(\boxed{
\frac{1}{2}(\Delta \alpha - \Delta \beta)}
\)
as shown in (c). The minus sign is needed because the counterclockwise rotation of \( ob \) is \( -\Delta \beta \). Using the assigned values, the rotation of the particle is then
\(\boxed{
\frac{1}{2}(6^\circ - (-4^\circ)) = 1^\circ}
\)
(Given the two rotations, taking the average is the only way we can measure the particle’s rotation, because any other approach would favor one side’s rotation over the other, which doesn’t make sense.)
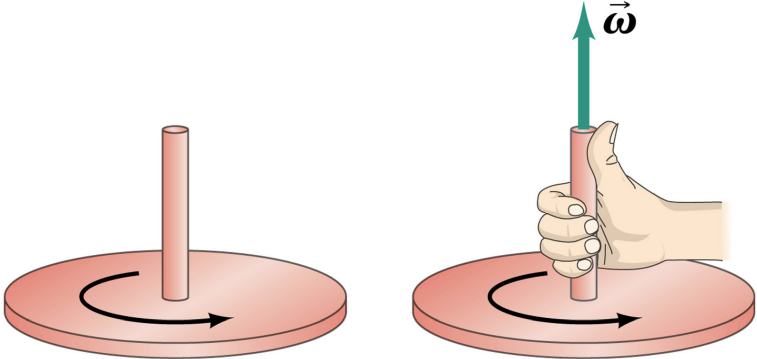
The angular velocity vector points along the axis of rotation; its direction is found using a right hand rule
1Fox and McDonald's Introduction to Fluid Mechanics, 8th Edition.
2Douglas C. Giancoli. Physics for Scientists & Engineers, 5th edition. 2022.