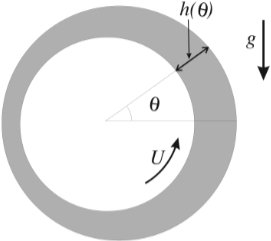
(2) Write down the boundary conditions at \(z=0\) and \(z=h(\theta)\) and show that \[ u(\theta, z) = U + \left( \frac{z^2}{2} - zh \right) \frac{g}{\nu} \cos(\theta) \] [3]
(3) Obtain an expression for the volume flux \[ Q(\theta) = \int_0^{h(\theta)} u \, dz \] across any section (with \(\theta = \text{constant}\)). Hence show that \[ \frac{1}{H^2} - \frac{1}{H^3} = \alpha \cos(\theta), \] where \[ H(\theta) = Uh(\theta)/Q, \qquad \alpha = \frac{gQ^2}{3\nu U^3}. \] Explain why \(Q\) is constant. [7]
(4) Find a perturbative solution for \(h(\theta)\) assuming \(\alpha \ll 1\), to first order in \(\alpha\). [hint: try a solution of the form \(H = A_0 + A_1[\alpha]\). [3]
(5) Show that a solution \(H(\theta)\) can exist for all values of \(\theta\) only if \(\alpha \leq 4/27\). [hint: it is easier to find the answer graphically]}. Show that the maximum film thickness the system can stably accommodate is \( h_{\text{max}} = \frac{3Q}{2H} \) Explain the physical mechanism behind this phenomenon. [5]
◀ ▶