For a Kelvin–Helmholtz instability in a continuously stratified ocean, obtain a globally integrated energy equation in the form:
\[
\frac{1}{2} \frac{d}{dt} \int \left( u^2 + w^2 + \frac{g^2 \rho^2}{\rho_0^2 N^2} \right) dV = - \int uw \frac{\partial U}{\partial z} dV.
\]
Discuss the physical meaning of each term and the mechanism of instability.
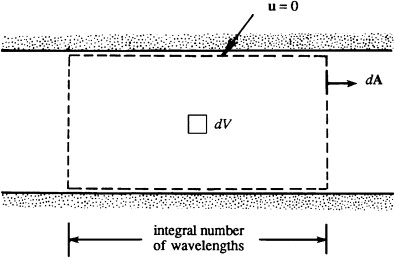
The integration in \(x\) takes place over an integer number of wavelengths.