Linear stability analysis: Consider the linear stability of this conducting state towards two-dimensional perturbations. The linearized equations: \(\boxed{ \frac{\partial}{\partial t} \nabla^2 \psi = -\text{Ra} \, \text{Pr} \, \frac{\partial \theta}{\partial x} + \text{Pr} \, \nabla^2 \psi}, \quad \) \(\boxed{ \frac{\partial \theta}{\partial t} = -\frac{\partial \psi}{\partial x} + \nabla^2 \theta} \) ,where \(\psi\) is the streamfunction of the perturbation
Solutions are sought in the form of normal modes \( q(x, y, t) = \hat{q}(y) e^{ikx + \lambda t} + c, \) where \(\lambda\) is the growth rate and \(k\) the perturbation’s wavenumber. Obtain the following generalized eigenvalue problem: \( \lambda \begin{bmatrix} D^2 - k^2 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \hat{\psi} \\ \hat{\theta} \end{bmatrix} = \begin{bmatrix} \text{Pr}(D^2 - k^2) & -ik \, \text{Ra} \, \text{Pr} \\ -ik & D^2 - k^2 \end{bmatrix} \begin{bmatrix} \hat{\psi} \\ \hat{\theta} \end{bmatrix} \) where \(D = d/dy\)
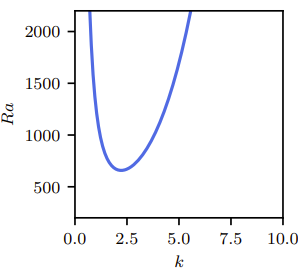
- Problem solved analytically in 1916 with free-slip boundary conditions, i.e. \( \psi(x, y, t) = \hat{\psi}(t) \sin(n \pi y) \sin(kx) \) \( \theta(x, y, t) = \hat{\theta}(t) \sin(n \pi y) \cos(kx) \)
- The dispersion relation reduces to a quadratic equation. One then obtains \( Ra_c = \frac{27 \pi^4}{4}, \quad k_c = \frac{\pi}{\sqrt{2}} \)
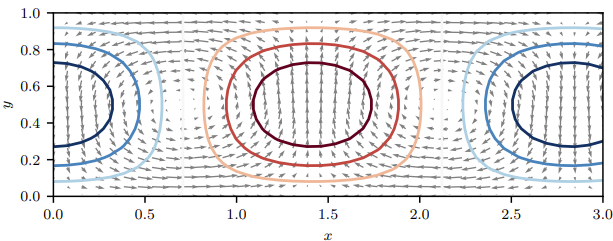
Isocontours of temperature and velocity field of the instability mode
1Jean-Christophe Loiseau. (2019). Chaotic convection and Lorenz-like dynamics. Machine Learning for Physics: Workshop III, IPAM Long Program.