The fixed points are \((\theta^*, v^*) = (k\pi, 0)\), where \(k\) is any integer. There's no physical difference between angles that differ by \(2\pi\), so we'll concentrate on the two fixed points \((0,0)\) and \((\pi,0)\). At \((0,0)\), the Jacobian is \( A = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \) so the origin is a linear center. The origin is a nonlinear center, for two reasons
The system is reversible: the equations are invariant under the transformation \(\tau \to -\tau,\; v \to -v\)
- The system is also conservative. Multiplying \( \ddot{\theta} + \sin \theta = 0 \) by \(\dot{\theta}\) and integrating yields \[ \dot{\theta}(\ddot{\theta} + \sin\theta) = 0 \Rightarrow \frac{1}{2}\dot{\theta}^2 - \cos\theta = \text{constant}. \]
The energy function \( E(\theta,v) = \frac{1}{2}v^2 - \cos\theta \) has a local minimum at \((0,0)\), since \(E \approx \frac{1}{2}(v^2 + \theta^2) - 1\) for small \((\theta,v)\). The origin is a nonlinear center. The closed orbits are approximately circular, with \(\theta^2 + v^2 \approx 2(E+1)\)
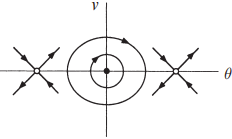
Consider the fixed point at \((\pi,0)\). The Jacobian is \( A = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}. \) The characteristic equation is \(\lambda^2 - 1 = 0\). Therefore \(\lambda_1 = -1,\;\lambda_2 = 1\); the fixed point is a saddle. The corresponding eigenvectors are \(\mathbf{v}_1 = (1,-1)\) and \(\mathbf{v}_2 = (1,1)\). The phase portrait near the fixed points can be sketched.
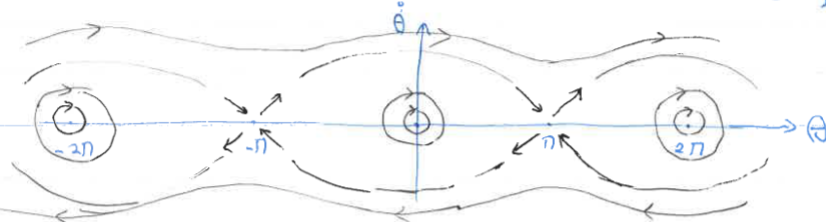
Include the energy contours \(E = \frac{1}{2}v^2 - \cos\theta\) for different values of \(E\). The picture is periodic in the \(\theta\)-direction. \( \ddot{\theta} + \sin{\theta} = 0 \rightarrow \begin{cases} \dot{\theta} = v \\ \dot{v} = -\sin{\theta} \end{cases} \rightarrow J = \begin{bmatrix} 0 & 1 \\[6pt] -\cos{\theta} & 0 \end{bmatrix} \rightarrow \lambda^2 = -\cos{\theta} \)
- \( \text{for } \theta = n\pi,\; n=\text{even} \quad\rightarrow\quad \lambda = \pm i \quad\text{center} \)
- \( \text{for } \theta = n\pi,\; n=\text{odd} \quad\rightarrow\quad \lambda = \pm 1 \quad\text{saddle}\quad u_1 = \begin{bmatrix}1 \\[4pt] 1\end{bmatrix},\quad u_2 = \begin{bmatrix}1 \\[4pt] -1\end{bmatrix} \)
1Strogatz, S.H. (2015). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (2nd ed.). CRC Press.