There are certain scientific situations where a fixed point must exist for all values of a parameter and can never be destroyed. For example, in the logistic equation and other simple models for the growth of a single species, there is a fixed point at zero population, regardless of the value of the growth rate. However, such a fixed point may change its stability as the parameter is varied. The transcritical bifurcation is the standard mechanism for such changes in stability
The normal form for a transcritical bifurcation is \( \dot{x} = rx - x^2 \)
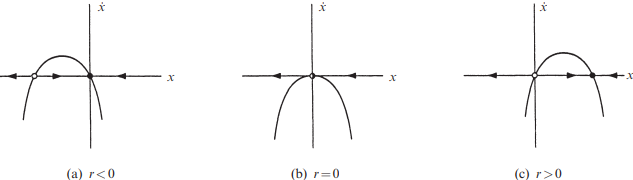
There is a fixed point at \( x^* = 0 \) for all values of \( r \)
The important difference between the saddle-node and transcritical bifurcations: in the transcritical case, the two fixed points don’t disappear after the bifurcation—instead they just switch their stability
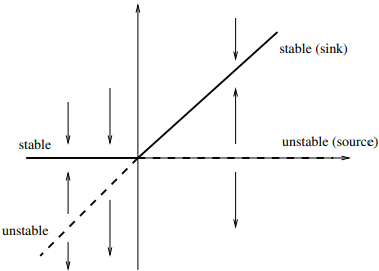
Transcritical bifurcation diagram
This equation is invariant under the change of variables \( x \rightarrow -x \)
1Strogatz, S.H. (2015). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (2nd ed.). CRC Press.
2Daniel Rothman. (2022). Nonlinear Dynamics: Chaos. MIT OpenCourseWare