The prototypical example of a saddle-node bifurcation is given by the first-order system \[ \dot{x} = r + x^2 \] where \( r \) is a parameter, which may be positive, negative, or zero. When \( r < 0 \), there are two fixed points, one stable and one unstable

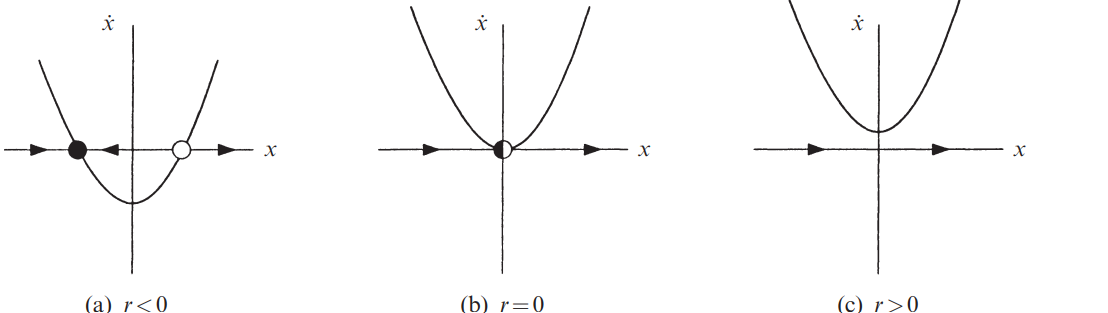
As \( r \) approaches 0 from below, the parabola moves up and the two fixed points move toward each other. When \( r = 0 \), the fixed points coalesce into a half-stable fixed point at \( x^* = 0 \). This type of fixed point is extremely delicate—it vanishes as soon as \( r > 0 \), and now there are no fixed points at all

In this example, a bifurcation occurred at \( r = 0 \), since the vector fields for \( r < 0 \) and \( r > 0 \) are qualitatively different