What can be said about the stability of a fixed point when \( f'(x^*) = 0 \)? Nothing can be said in general.
The stability is best determined on a case-by-case basis, using graphical methods. Consider
- (a) \(\quad \dot{x} = -x^3 \quad\quad\)
- (b) \(\quad \dot{x} = x^3 \quad\quad\)
- (c) \(\quad \dot{x} = x^2 \quad\quad\)
- (d) \(\quad \dot{x} = 0 \quad\quad\)
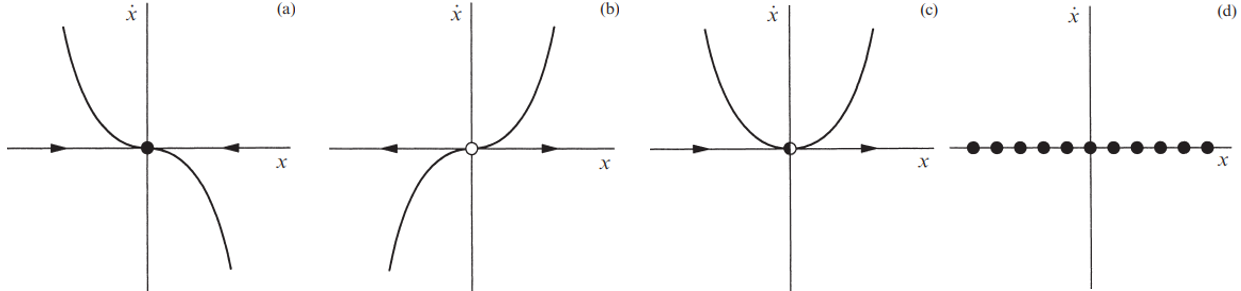
Each of these systems has a fixed point \( x^* = 0 \) with \( f'(x^*) = 0 \). However the stability is different in each case. Case (a) is stable and (b) is unstable. Case (c) is a hybrid case half-stable, since the fixed point is attracting from the left and repelling from the right, we therefore indicate this type of fixed point by a half-filled circle. Case (d) is a whole line of fixed points; perturbations neither grow nor decay.
They arise naturally in the context of bifurcations
1Strogatz, S.H. (2015). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (2nd ed.). CRC Press.