Now we explain the physical meaning of the mixing-length hypothesis.

Consider a statistically steady and statistically uniform turbulent shear flow in which the mean velocity has only a streamwise component $U$ that varies only with the normal coordinate $y$. At time $t$, a unit-volume fluid parcel located at $(x,y,z)$ has a streamwise momentum component $\rho\,\tilde{u}(x,y,z,t)$, where $\tilde{u}$ denotes the streamwise velocity component associated with the irregular turbulent motion. Because of turbulence, this parcel moves to $(x+\Delta x,\; y+\Delta y,\; z+\Delta z)$ at time $t+\Delta t$, and during the interval $\Delta t$ it is assumed not to change its original momentum

At $t+\Delta t$ the momentum defect of this parcel relative to the surrounding fluid is $$ \Delta m \;=\; \rho\,\tilde{u}(x+\Delta x,\; y+\Delta y,\; z+\Delta z,\; t+\Delta t) \;-\;\rho\,\tilde{u}(x,\; y,\; z,\; t) $$

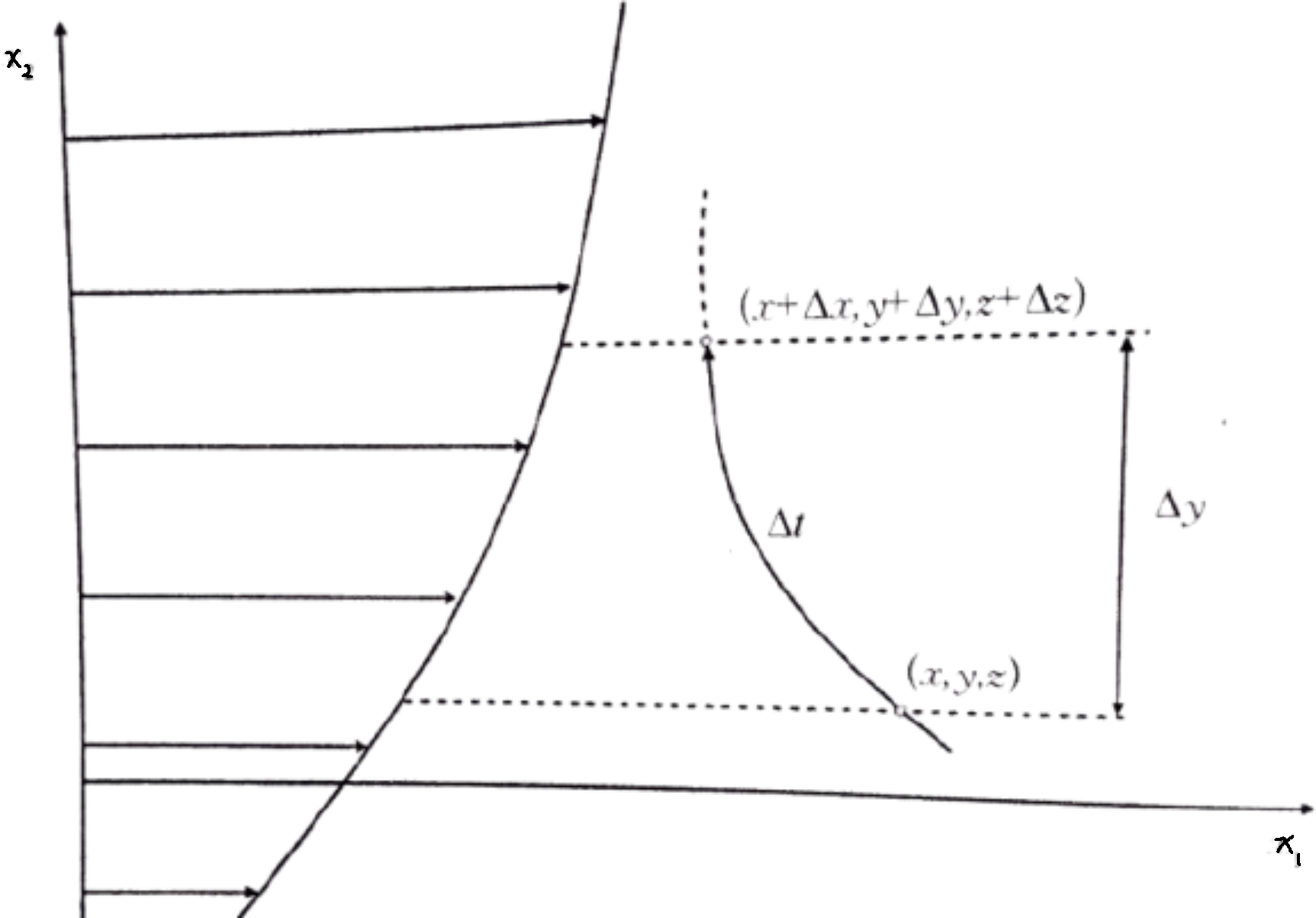
The volumetric flux across a unit area in the normal direction caused by the turbulent fluctuation is $v$. Therefore, per unit time, the statistical average of the streamwise momentum defect transported by turbulence through a unit area at $y+\Delta y$, namely the Reynolds shear-stress component $$ -\rho\,\overline{uv} \;=\;\rho\,\overline{\,v\,\Delta y\,}\,\frac{\partial U}{\partial y} $$ where the overbar denotes an ensemble average over all fluid parcels that, starting from the position $y$, undergo turbulent displacements in the wall-normal direction. Let the mean of this distance be the mixing length $\ell$, and let $v^{*}=(\overline{v^{2}})^{1/2}$ $$ -\rho\,\overline{u\,v}=C\,\rho\,v^{*}\,\ell\,\frac{\partial U}{\partial y} $$ where $C$ is a constant. Thus we recover the eddy-viscosity coefficient $\nu_t=C\,v^{*}\ell$