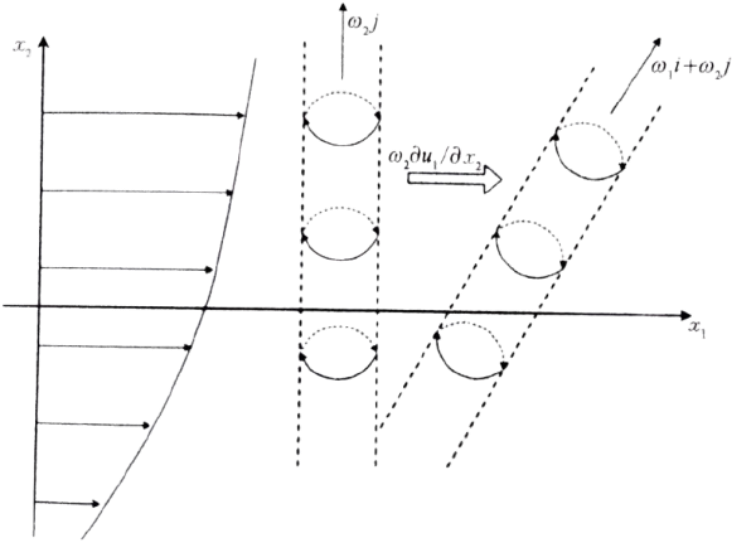
To construct a turbulent viscosity model, the eddy-viscosity coefficient $\nu_t$ should be represented approximately by scale variables of the turbulence. Turbulence is multi-scale

A turbulent flow contains at least three typical scales the scale of the mean flow the scale of the energy-containing eddies in the inertial range the scale of the dissipative eddies (also called the Kolmogorov scale). For fully developed turbulence far from solid walls, it is reasonable to assume that the characteristics of the turbulent motion depend mainly on the length scale $\ell$ and time scale $\tau$ of the energy-containing eddies in the inertial range. Through dimensional analysis $$ \nu_t \propto l^{2}\tau^{-1},\qquad k \propto l^{2}\tau^{-2},\qquad \varepsilon \propto l^{2}\tau^{-3},\qquad \frac{\overline{\omega_i\omega_i}}{2}\propto \tau^{-2},\qquad \cdots $$ where $k$ is the turbulent kinetic energy per unit mass, $\varepsilon$ the dissipation rate of turbulent kinetic energy, and $\omega_i\omega_i/2$ the enstrophy