Using \(p'=\hat{p}(z)\exp\{i(kx+ly-\omega t)\}\) and \(\hat{p}=A\cosh[\alpha(z-H/2)]+B\sinh[\alpha(z-H/2)
\), the two boundary conditions require
$$
A \left[\alpha c \sinh \frac{\alpha H}{2} - \frac{U_0}{H} \cosh \frac{\alpha H}{2}\right]
+ B \left[- \alpha c \cosh \frac{\alpha H}{2} + \frac{U_0}{H} \sinh \frac{\alpha H}{2}\right] = 0
$$
$$
A \left[\alpha (U_0 - c) \sinh \frac{\alpha H}{2} - \frac{U_0}{H} \cosh \frac{\alpha H}{2}\right]
+ B \left[\alpha (U_0 - c) \cosh \frac{\alpha H}{2} - \frac{U_0}{H} \sinh \frac{\alpha H}{2}\right] = 0
$$
where $c = \omega / k$ is the eastward phase velocity
This is a pair of homogeneous equations for the constants $A$ and $B$.
For non-trivial solutions to exist, the determinant of the coefficients must vanish.
This gives the phase velocity
$$
c = \frac{U_0}{2} \pm \frac{U_0}{\alpha H}
\sqrt{\left(\frac{\alpha H}{2} - \tanh \frac{\alpha H}{2}\right)
\left(\frac{\alpha H}{2} - \coth \frac{\alpha H}{2}\right)}
$$
Whether the solution grows with time depends on the sign of the radicand
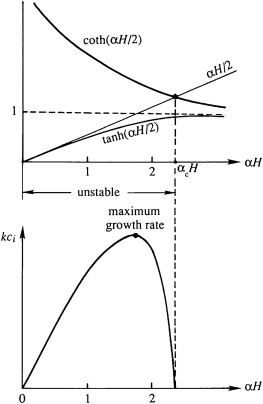
Baroclinic instability.
The upper panel shows behavior of the functions in \(c = \frac{U_0}{2} \pm \frac{U_0}{\alpha H}
\sqrt{\left(\frac{\alpha H}{2} - \tanh \frac{\alpha H}{2}\right)
\left(\frac{\alpha H}{2} - \coth \frac{\alpha H}{2}\right)}\) and the lower panel shows growth rates of unstable waves.
The first factor in the radicand is positive because $\alpha H / 2 > \tanh (\alpha H / 2)$ for all values of $\alpha H$.
However, the second factor is negative for small values of $\alpha H$ for which $\alpha H / 2 < \coth (\alpha H / 2)$.
In this range, the roots of $c$ are complex conjugates, with $c = U_0 / 2 \pm i c_i$.
Because we have assumed that the perturbations are of the form $\exp (-ikct)$,
the existence of a non-zero $c_i$ implies the possibility of a perturbation that grows as $\exp (kc_i t)$,
and the solution is unstable
◀
▶
