Perturbation Vorticity Equation
$$
\frac{\partial \rho'}{\partial t}+U\frac{\partial \rho'}{\partial x}+v'\frac{\partial \overline{\rho}}{\partial y}
-\rho_0 N^2 \frac{w'}{g}=0
$$
The pressure is presumed to be hydrostatic
$$
0=-\frac{\partial p'}{\partial z}-\rho' g \Rightarrow w'=-\frac{1}{\rho_0 N^2}\!\left[\left(\frac{\partial}{\partial t}+U\frac{\partial}{\partial x}\right)\frac{\partial p'}{\partial z}
-\frac{dU}{dz}\frac{\partial p'}{\partial x}\right]
$$
where the thermal wind relation \(\frac{d U}{d z} = \frac{g}{\rho_0 f} \frac{\partial \bar{\rho}}{\partial y}
\) has been used to write $\partial \overline{\rho}/\partial y$ in terms of the thermal wind $dU/dz$
\(\Rightarrow\) With the perturbation vorticity \(\boxed{\zeta' = \frac{1}{\rho_0 f} \left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} \right) p'
= \frac{1}{\rho_0 f} \nabla_H^2 p'}\), the perturbation vorticity equation \(\boxed{\frac{\partial \zeta}{\partial t}+u\frac{\partial \zeta}{\partial x}+v\frac{\partial \zeta}{\partial y}
-(\zeta+f)\frac{\partial w}{\partial z}=0}\) becomes
$$
\left(\frac{\partial}{\partial t}+U\frac{\partial}{\partial x}\right)
\left[\nabla_H^2 p'+\frac{f^2}{N^2}\frac{\partial^2 p'}{\partial z^2}\right]=0
$$
This is the equation that governs quasi-geostrophic perturbations on an eastward flow $U(z)$
This animation shows baroclinic instability in a full 3D model
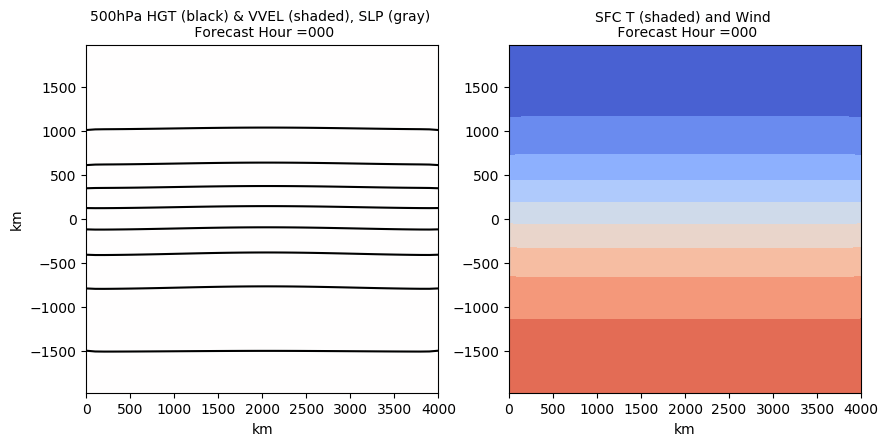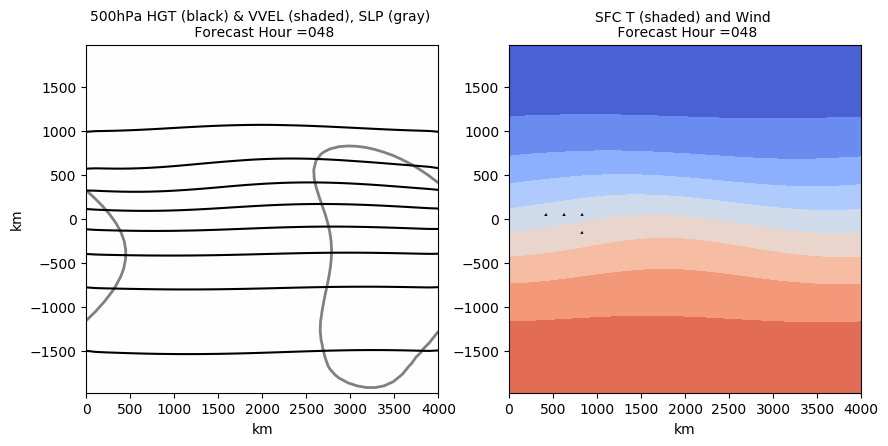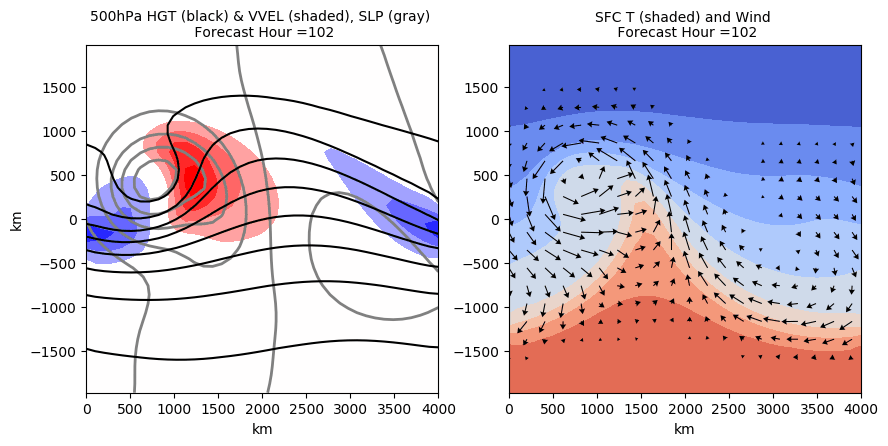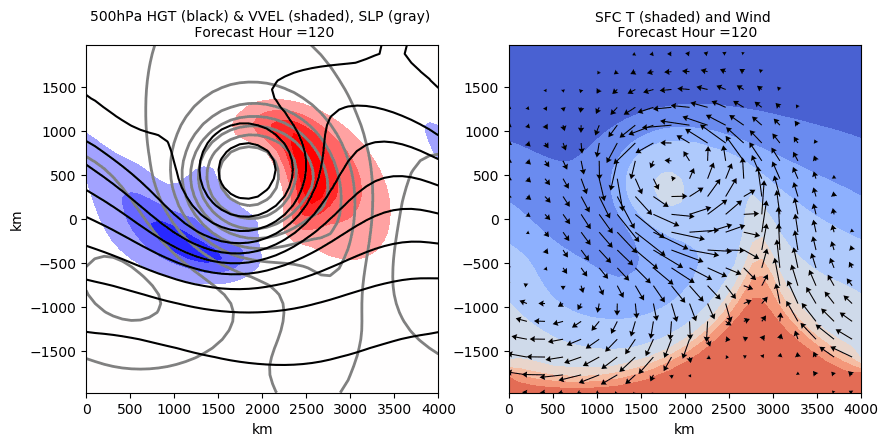
1Dr. Mathew Barlow. May 14, 2020. Weather Center UMass Lowell. Gallery Of Atmospheric Dynamics Animations.
https://storm.uml.edu/~metweb/newBlog/wordpress/2020/05/14/gallery-of-atmospheric-dynamics-animations/