Barotropic Instability
Comparing the perturbation vorticity equation \(\boxed{(U - c)\left[\frac{d^{2}}{dy^{2}} - k^{2}\right] \hat{\psi} +
\left[\beta - \frac{d^{2}U}{dy^{2}}\right] \hat{\psi} = 0}\) with the Rayleigh equation \(\boxed{(U - c) \left( \frac{d^{2}\phi}{dy^{2}} - k^{2}\phi \right)
- \frac{d^{2}U}{dy^{2}} \phi = 0}\) derived without the Coriolis acceleration,
the effect of planetary rotation is the replacement of $-d^{2}U/dy^{2}$ by $(\beta - d^{2}U/dy^{2})$
A necessary condition for the inviscid instability of a barotropic current $U(y)$
is that the gradient of the absolute vorticity
$$
\frac{d}{dy} \bigl(\bar{\zeta} + f\bigr) = - \frac{d^{2}U}{dy^{2}} + \beta
$$
must change sign somewhere in the flow
Barotropic instability quite possibly plays an important role in the instability of currents in the atmosphere and in the ocean. The instability has no preference for any latitude, because the criterion involves $\beta$ and not $f$. However, the mechanism presumably dominates in the tropics because mid-latitude disturbances prefer the baroclinic instability mechanism. An unstable distribution of westward tropical wind is shown below.
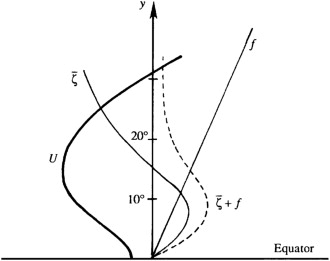
Profiles of velocity $U(y)$, vorticity $\bar{\zeta}$, and Coriolis parameter $f$ in a westward tropical wind as a function of latitude. The velocity distribution is barotropically unstable as $d(\bar{\zeta} + f)/dy$ changes sign within the flow near $8^{\circ}$