- their geometries are scale similar
- their dimensionless parameters match
[Ex] Consider the drag force $F_D$ on a sphere, of diameter $d$ moving at a speed $U$ through a fluid of density $\rho$ and viscosity $\mu$. Dimensional analysis using these five parameters produces the following possible dimensionless scaling laws: \[\frac{F_D}{\rho U^2 d^2} = \Psi \left( \frac{\rho U d}{\mu} \right)\]
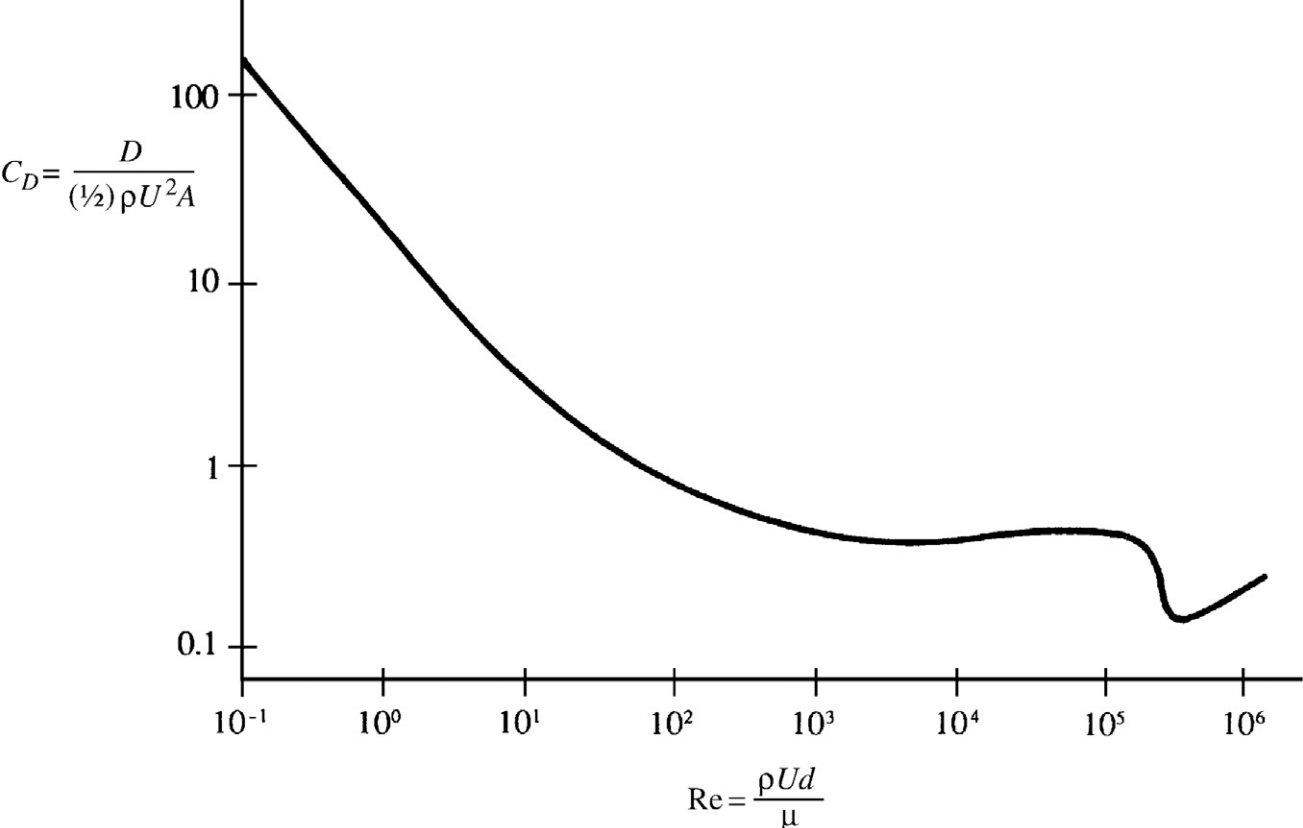
Coefficient of drag $C_D$ for a sphere vs. the Reynolds number Re based on sphere diameter. At low Reynolds number $C_D \sim 1/\text{Re}$, and above $\text{Re} \sim 10^3$, $C_D \sim$ constant (except for the dip between $\text{Re} = 10^5$ and $10^6$). These behaviors (except for the dip) can be explained by simple dimensional reasoning. The reason for the dip is the transition of the laminar boundary layer to a turbulent one.