Using Viscosity Instead of Drag

When adding both western and eastern boundary layer corrections, the full solution is written as $$ \hat{\psi} = \psi_I - e^{-\hat{x}/(2\epsilon)} \Bigg\{ \psi_I(0,\hat{y}) \Bigg[\cos\!\left(\tfrac{\sqrt{3}\hat{x}}{2\epsilon}\right) + \tfrac{1}{\sqrt{3}}\sin\!\left(\tfrac{\sqrt{3}\hat{x}}{2\epsilon}\right)\Bigg] + \tfrac{2\epsilon}{\sqrt{3}} \sin\!\left(\tfrac{\sqrt{3}\hat{x}}{2\epsilon}\right) \left.\frac{\partial \psi_I}{\partial \hat{x}}\right|_{x=0} \Bigg\} - \epsilon e^{(\hat{x}-1)/\epsilon} \left.\frac{\partial \psi_I}{\partial \hat{x}}\right|_{x=1} $$ where $\epsilon = (\nu / \beta a^3)^{1/3}$

With the canonical wind stress, using the interior (Sverdrup) solution $$ \psi_I = \pi (1-x)\sin \pi y $$ This simplifies the interior contributions and yields $$ \hat{\psi} = \pi \sin(\pi \hat{y}) \Bigg\{ 1-\hat{x} - e^{-\hat{x}/(2\epsilon)} \Bigg[\cos\!\left(\tfrac{\sqrt{3}\hat{x}}{2\epsilon}\right) + \tfrac{1-2\epsilon}{\sqrt{3}} \sin\!\left(\tfrac{\sqrt{3}\hat{x}}{2\epsilon}\right)\Bigg] + \epsilon e^{(\hat{x}-1)/\epsilon} \Bigg\} $$

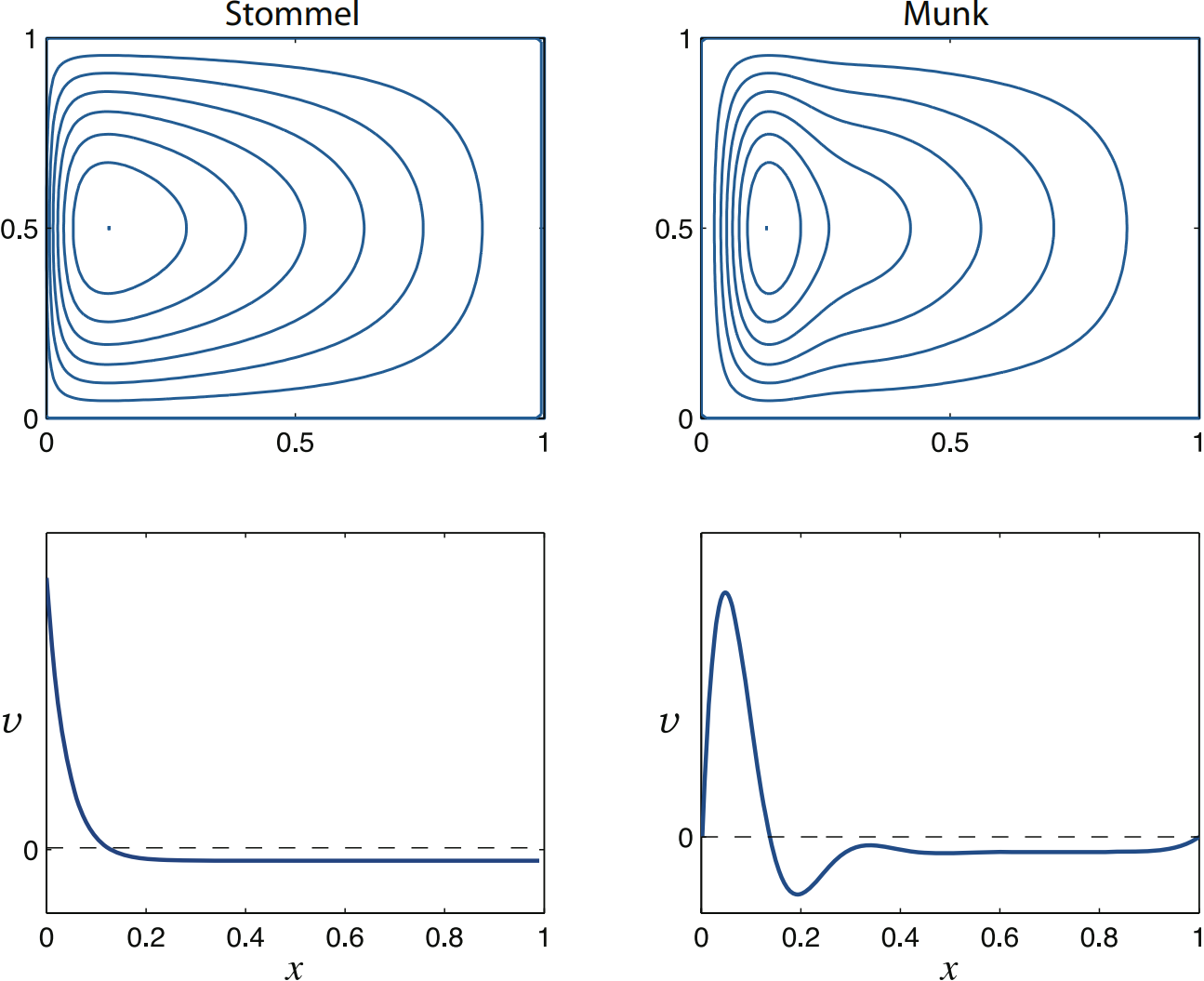
The Stommel and Munk solutions, with the wind stress $\tau = -\cos \pi y$, for $x,y \in (0,1)$. Upper panels are contours of streamfunction in the $x$-$y$ plane, and the flow is clockwise. The lower panels are plots of meridional velocity, $v$, as a function of $x$, in the centre of the domain.
The Munk layers bring the tangential as well as the normal velocity to zero. The eastern boundary layer has a similar thickness to the western boundary layer, but is not as dynamically important since its raison d'etre is to enable the no-slip condition to be satisfied, a relatively weak frictional constraint that manifests itself by a boundary layer in which the flow parallel to the boundary is slowed down.
The western boundary layer exists in order that the no-normal flow condition can be satisfied, which causes a qualitative change in the flow pattern.

¹Vallis, G.K. (2017) Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation. 2nd edn. Cambridge: Cambridge University Press.

◀ ▶