Approximate Solution of the Stommel Model: Asymptotic Matching

$$ \psi = \frac{\tau_0 \pi}{\beta} \left(1 - \frac{x}{a} - e^{-x/(a\epsilon_S)}\right) \sin \frac{\pi y}{a} $$ This is a 'single gyre' solution. Two or more gyres can be obtained with a different wind forcing, such as $\tau^x = -\tau_0 \cos(2 \pi y)$

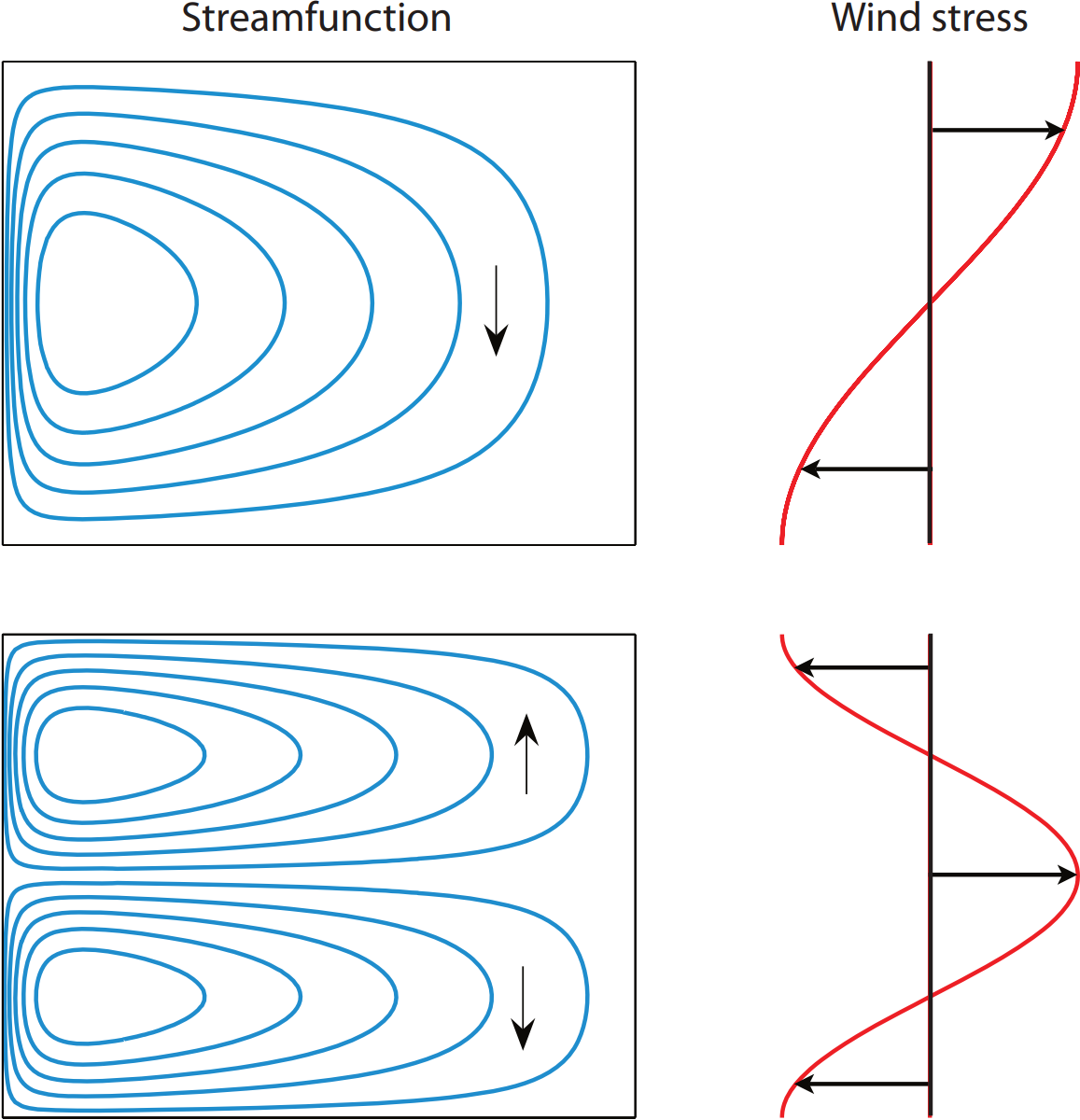
Two solutions of the Stommel model. Upper panel shows the streamfunction of a single-gyre solution, with a wind stress proportional to $-\cos(\pi y / a)$ (in a domain of side $a$), and the lower panel shows a two-gyre solution, with wind stress proportional to $\cos(2 \pi y / a)$
It is a relatively straightforward matter to generalize to other wind stresses, provided these also vanish at the two latitudes between which the solution is desired. In general $$ \psi_I = \int_{x_E}^x \text{curl}_z \tau(x',y)\, dx' $$ and that the composite solution is $$ \psi = \psi_I - \psi_I(0,y) e^{-x/(x_E \epsilon_S)} $$

¹Vallis, G.K. (2017) Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation. 2nd edn. Cambridge: Cambridge University Press.

◀ ▶