Reynolds averaging has been done already, and $k$ is turbulent diffusivity
$f = 2\Omega \sin\Theta, \text{ where } \Omega = \frac{2\pi}{\text{day}} = \frac{2\pi}{86400 \, \text{s}} \text{ and } \Theta \text{ is latitude}$
For now, we avoid using the spherical coordinate system, so we use Taylor $ f(x) \approx f(x_0) + f'(x_0)\Delta x $ to approximate f: $ f = f_{o} + \left. \frac{\partial f}{\partial \theta} \right|_{\theta_{o}} \Delta \theta + \left. \frac{\partial^{2} f}{\partial \theta^{2}} \right|_{\theta_{o}} \frac{\Delta \theta^{2}}{2} + \cdots = 2 \Omega \sin \theta_{o} + 2 \Omega \cos \theta_{o} (\theta - \theta_{o}) + \mathcal{O}(\Delta \theta^{2}) = \boxed{f_{o} + \beta y} $

Zonal (East–West) Momentum Equation: \[ \frac{\partial u}{\partial t} + \vec{u} \cdot \nabla u - fv = -\frac{1}{\rho_0} \frac{\partial p}{\partial x} + \nu \nabla^2 u + \underbrace{F^x}_{\substack{\text{External forcing in the $x$-direction} \\ \text{(typically wind stress $\tau^x$)}}}\]
Meridional (North–South) Momentum Equation: \[\frac{\partial v}{\partial t} + \vec{u} \cdot \nabla v + fu = -\frac{1}{\rho_0} \frac{\partial p}{\partial y} + \nu \nabla^2 v + \underbrace{F^y}_{\substack{\text{External forcing in the $y$-direction} \\ \text{(typically wind stress $\tau^y$)}}}\]
Hydrostatic Balance (Vertical):\[\frac{\partial p}{\partial z} = -\rho g \]
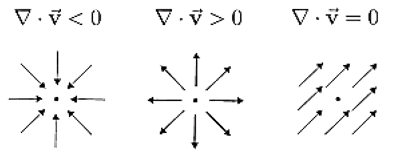
Continuity (Incompressibility): \[ \nabla \cdot \vec{u} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 \]

◀ ▶