$$ \underbrace{M_x}_{\substack{\text{zonal mass transport in the}\\\text{wind–driven layer}}} = \int_{-D}^{0} \rho u(z) \, dz, \qquad \underbrace{M_y}_{\substack{\text{meridional mass transport in the}\\\text{wind–driven layer}}} = \int_{-D}^{0} \rho v(z) \, dz $$

Streamfunction representation of volume transport 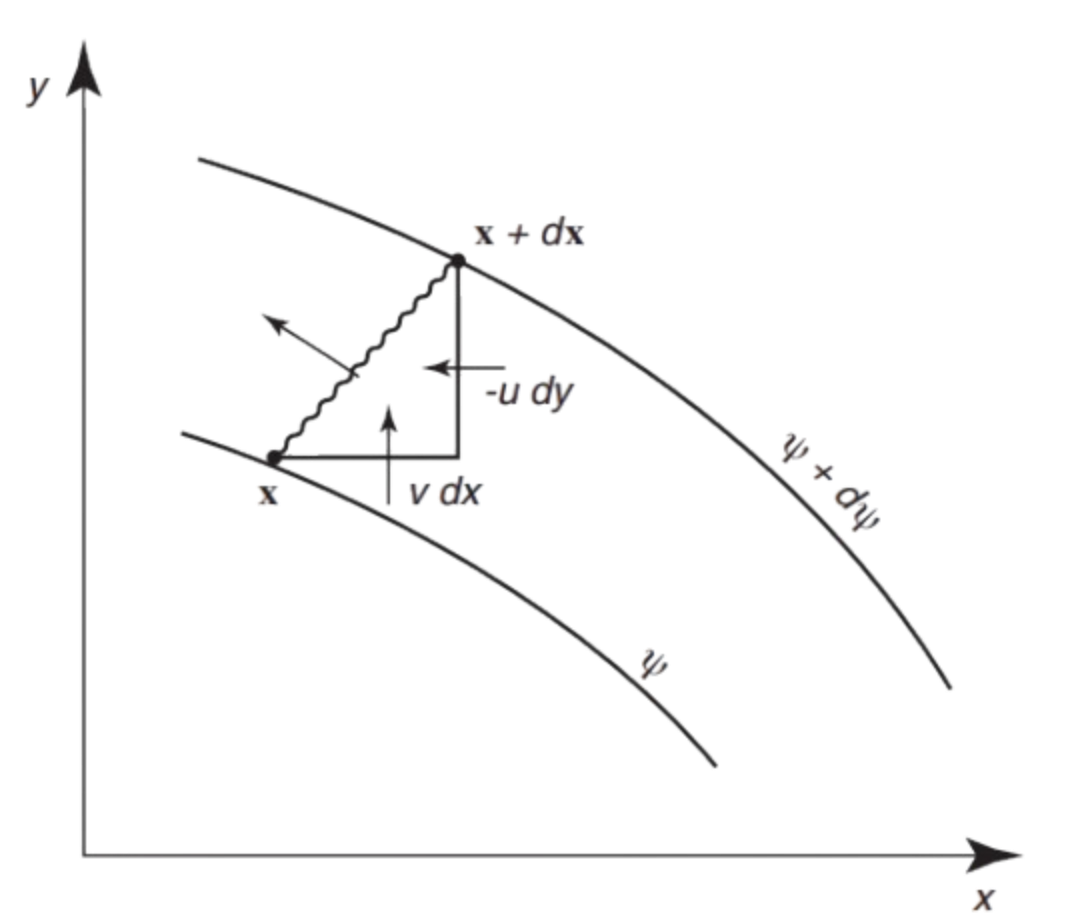$$ U = - \frac{\partial \Psi}{\partial y}, \qquad V = \frac{\partial \Psi}{\partial x} $$

Integrating westward from the eastern boundary $$ \Psi(x,y) = \frac{1}{\rho_{\text{ref}} \, \beta} \int_{\text{eastern bdy}}^{x} \underbrace{\hat{\mathbf{z}}}_{\substack{\text{vertical}\\\text{unit vector}}} \cdot \underbrace{\left( \nabla \times \boldsymbol{\tau}_{\text{wind}} \right)}_{\substack{\text{curl of}\\\text{wind stress}}} \, dx $$