Geostrophy

If both the Ekman number and the Rossby number are small, the first approximation to the momentum equation is $$ \rho \, 2\Omega \times \mathbf{u} = - \nabla p + \rho \nabla \Phi $$

Large-scale ocean flows generally follow geostrophic balance
$x$-direction:$fv = \frac{1}{\rho}\,\frac{\partial p}{\partial x}$ $y$-direction:$fu = -\frac{1}{\rho}\,\frac{\partial p}{\partial y}$

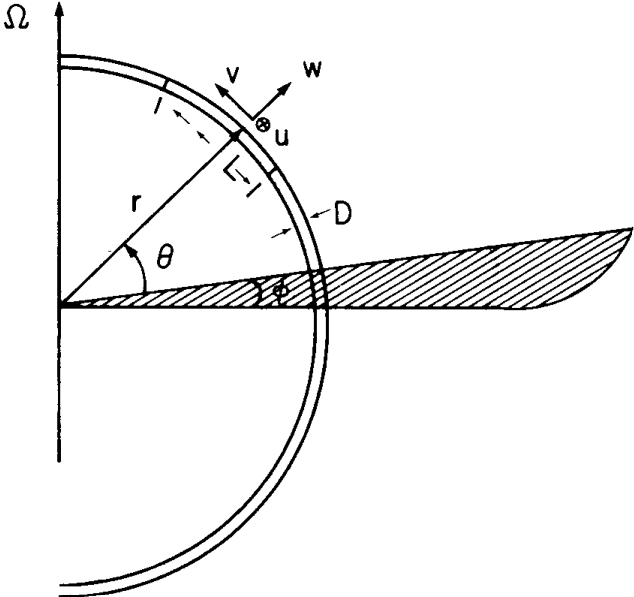
$$ \rho\Big[ -2 \Omega \underbrace{v}_{\text{northward velocity}} \sin\theta + 2\Omega \underbrace{w}_{\text{vertical velocity}} \cos\theta \Big] = -\frac{1}{r \cos\theta} \frac{\partial p}{\partial \underbrace{\phi}_{\text{longitude}}} $$ $$ \rho \, 2\Omega \underbrace{u}_{\text{eastward velocity}} \sin\theta = -\frac{1}{r} \frac{\partial p}{\partial \underbrace{\theta}_{\text{colatitude}}} $$ $$ -\rho \, 2\Omega u \cos\theta = -\frac{\partial p}{\partial r} - \rho \overbrace{g}^{\text{gravitational acceleration}} $$

In the absence of relative motion $u = v = w = 0$, the equation implies that $p$ must be independent of $\phi$ and $\theta$ and therefore be a function only of $r$. The density must also be a function only of $r$
$ p = p_s(r) + p'(r, \theta, \phi) $
$ \rho = \rho_s(r) + \rho'(r, \theta, \phi) $
where $p_s(r)$ and $\rho_s(r)$ are the fields that would be present in the absence of motion, while $p'$ and $\rho'$ are the departures from this basic state due to the existence of winds and currents.

$ - \frac{\partial p_s}{\partial r} = \rho_s g \;\;\Rightarrow\;\; \begin{cases} (\rho_s + \rho')\big[-2\Omega v \sin\theta + 2\Omega w \cos\theta\big] = - \dfrac{1}{r \cos\theta}\dfrac{\partial p'}{\partial \phi} &\\ (\rho_s + \rho') 2\Omega u \sin\theta = - \dfrac{1}{r}\dfrac{\partial p'}{\partial \theta} &\\ -(\rho_s + \rho') 2\Omega u \cos\theta = - \dfrac{\partial p'}{\partial r} - \rho' g \end{cases} $

¹ Pedlosky, J. (1982). Geophysical Fluid Dynamics. Springer study edition. Springer, Berlin, Heidelberg.

◀ ▶