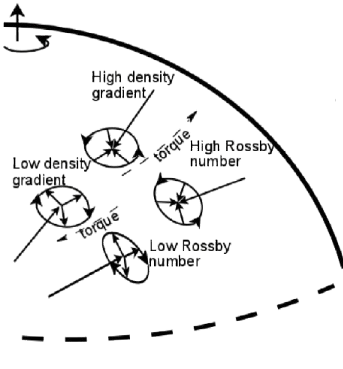
$$ \begin{aligned} &\text{Rossby number} = \frac{U}{fL} \\ &= \begin{cases} \ll 1 & \text{Coriolis force dominates} \\ \sim 1 & \text{Advection and Coriolis are comparable} \\ \gg 1 & \text{Advection dominates; rotation negligible} \end{cases} \end{aligned} $$

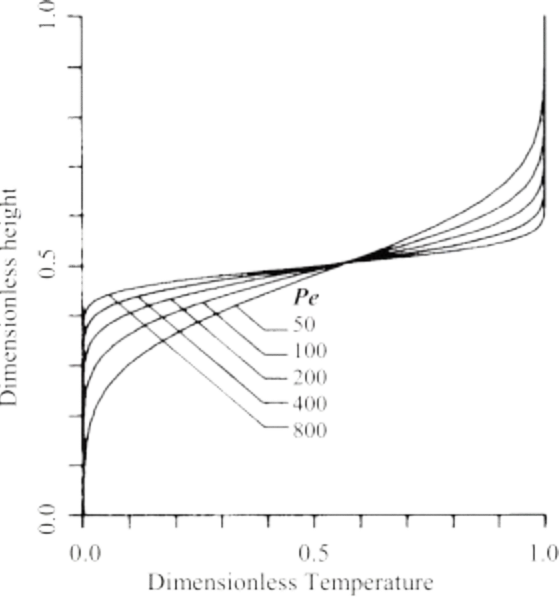
$$ \begin{aligned} &\text{Péclet number} = \frac{UL}{k} \\ &= \begin{cases} \ll 1 & \text{Diffusion dominates (slow, smoothed transport)} \\ \sim 1 & \text{Advection and diffusion are both important} \\ \gg 1 & \text{Advection dominates (sharp gradients persist)} \end{cases} \end{aligned} $$

$ \begin{aligned} \mathcal{O}\left( \frac{u \, \frac{\partial DIC}{\partial x}}{k \, \frac{\partial^2 DIC}{\partial x^2}} \right) &= \mathcal{O}\left( \frac{u}{k} \cdot \frac{\frac{\partial DIC}{\partial x}}{\frac{\partial^2 DIC}{\partial x^2}} \right) \approx \mathcal{O}\left( \frac{u}{k} \cdot \frac{\Delta DIC / \Delta x}{\Delta DIC / \Delta x^2} \right) = \mathcal{O}\left( \frac{u}{k} \cdot \frac{\Delta DIC / \Delta x}{\Delta DIC / (\Delta x)^2} \right) = \mathcal{O}\left( \frac{u}{k} \cdot \frac{(\Delta x)^2}{\Delta x} \right) \\[8pt] = \mathcal{O}\left( \frac{u \cdot \Delta x}{k} \right) &\approx \mathcal{O}\left( \frac{U \cdot L}{k} \right) = \mathcal{O}\left( \frac{UL}{k} \right) \end{aligned} $

with $ U = 1 \times 10^{-4} \, \text{m/s}, \quad L = 1 \times 10^6 \, \text{m}, \quad k = 1 \times 10^2 \, \text{m}^2/\text{s} \Rightarrow \text{Pe} \approx 1 $