Let the characteristic magnitude of \( u \) be \( U_{\infty} \), the velocity at a large distance upstream of the body, and let \( L \) be the stream-wise distance over which \( u \) changes appreciably. The longitudinal length of the body can serve as \( L \), because \( u \) within the boundary layer may change in the stream-wise direction by a large fraction of \( U_{\infty} \) over a distance \( L \)

A measure of \( \partial u / \partial x \) is therefore \( U_{\infty}/L \), so that the approximate size of the first advective term in \[\frac{D\mathbf{u}}{Dt} = -\frac{1}{\rho} \nabla p + \nu \nabla^2 \mathbf{u}\] is \[u \left( \frac{\partial u}{\partial x} \right) \sim \frac{U_{\infty}^2}{L}\] where \( \sim \) is to be interpreted as "of order"

The approximate size of the viscous stress term in \( u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = -\frac{1}{\rho} \frac{\partial p}{\partial x} + \nu \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right) \) is \[ \left(\frac{1}{\rho} \right) \left(\frac{\partial \tau}{\partial y} \right) = \nu \left( \frac{\partial^2 u}{\partial y^2} \right) \sim \frac{\nu U_{\infty}}{\bar{\delta}^2} \] \( \tau \) represents the shear stress in the fluid, specifically the viscous shear stress in the boundary layer

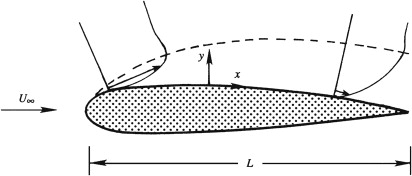
Velocity profiles at two positions within the boundary layer. The boundary-layer thickness is greatly exaggerated

The two velocity vectors are drawn at the same distance \( y \) from the surface, showing that the variation of \( u \) over a distance \( x \sim L \) is of the order of the free-stream velocity \( U_{\infty} \)

◀ ▶