Boundary Layer Theory
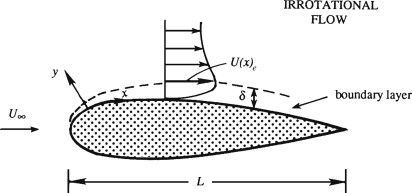
A boundary layer forms when a viscous fluid moves over a solid surface. Only the boundary layer on the top surface of the foil is depicted in the figure and its thickness, \( \delta \), is greatly exaggerated
\( U_{\infty} \) is the oncoming free-stream velocity and \( U_e \) is the velocity at the edge of the boundary layer. The usual boundary layer coordinate system allows the \( x \)-axis to coincide with a mildly curved surface so that the \( y \)-axis lies in the surface-normal direction
1Argyris G. Panaras, Frank K. Lu. (2015). Micro-vortex generators for shock wave/boundary layer interactions. Progress in Aerospace Sciences.