The difference in form between the Reynolds equation and the Navier–Stokes (N–S) equations lies in the appearance of the Reynolds stress term $\overline{u_i' u_j'}$. From the perspective of statistical averaging, the Reynolds equation still contains all the information of turbulent motion. The Reynolds stress has the following characteristics:

• The Reynolds stress is an unknown term in the equation, arising from the nonlinearity of the N–S equations $$ \overline{\left( \frac{D u_i}{D t} \right)} = \overline{\left( \frac{\partial \tilde{u}_i}{\partial t} \right)} + \overline{\left( \tilde{u}_j \frac{\partial \tilde{u}_i}{\partial x_j} \right)} = \frac{\partial U_i}{\partial t} + U_j \frac{\partial U_i}{\partial x_j} + \frac{\partial \overline{u_i' u_j'}}{\partial x_j} $$ The effect of Reynolds averaging shows the influence of velocity fluctuations on the mean flow field.
• After moving the Reynolds stress term to the right-hand side of the equation, in physical terms it can be regarded as an additional stress. Similar to viscous stress, its shear acts on the mean flow field, thereby altering momentum transport.
• The Reynolds stress tensor is symmetric, $$ \overline{u_i u_j} = \overline{u_j u_i} $$ Its components $\overline{u^2}, \overline{v^2}, \overline{w^2}$ are normal stresses and can also be regarded as the three energy components of turbulent motion. The cross-correlation terms $\overline{uv}, \overline{uw}, \overline{vw}$ are shear Reynolds stresses, which have an important influence on the distribution of the mean velocity profile.
• 

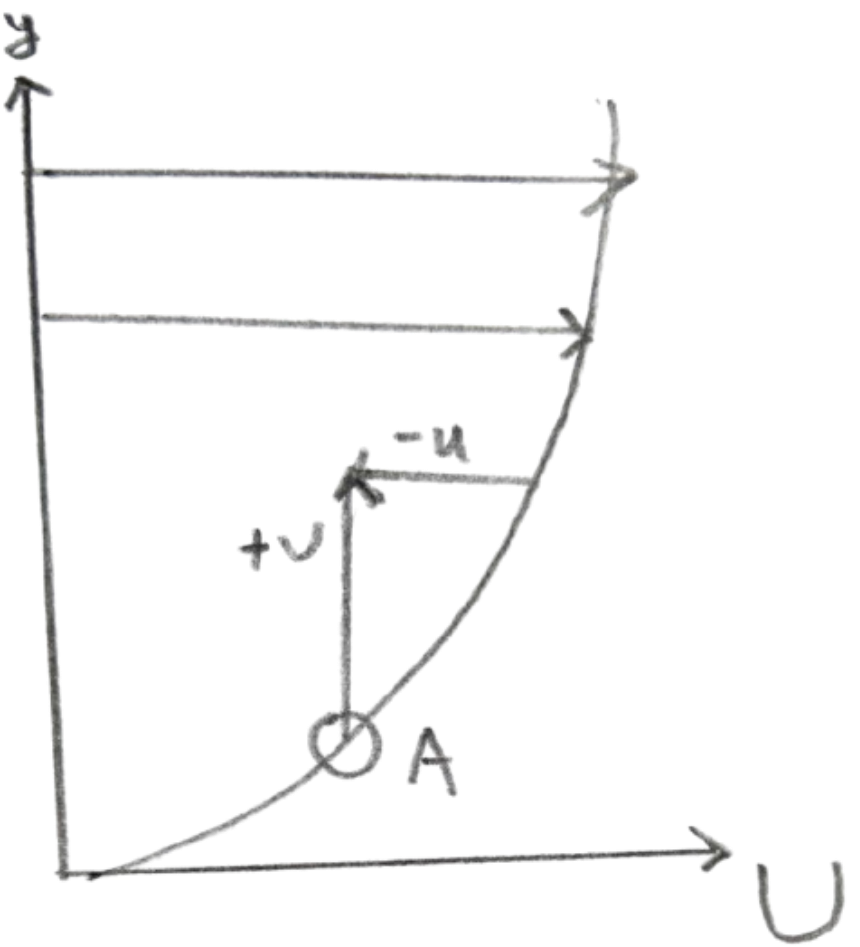
  The fluctuating velocity correlations bring about momentum transfer (the effect of additional stress). Consider a mean flow field with $\partial U/\partial y > 0$. At point A, if a fluid particle has a positive velocity fluctuation $v$, it will bring low-momentum fluid into a high-momentum region, resulting in a negative $u$ fluctuation. Similarly, for a negative $v$ fluctuation, a positive $u$ fluctuation is also likely to occur. Therefore, when $\partial U/\partial y > 0$, $\overline{uv}$ is usually negative, producing a momentum flux in the negative $y$ direction.

◀ ▶