In summary, the simplifications of the boundary-layer assumption are as follows

Diffusion in the stream-wise direction is negligible compared to that in the wall-normal direction
The pressure in the boundary layer can be found from the outer flow, so that it is regarded as a known quantity within the boundary layer that does not vary perpendicular to the surface
A crude estimate of the wall shear stress $\tau_w$,, can be made from the various scalings employed earlier:$\boxed{\tau_w \sim \mu\,\frac{U}{\delta}\ \sim\ \left(\frac{\mu U}{L}\right)\mathrm{Re}^{1/2}}$

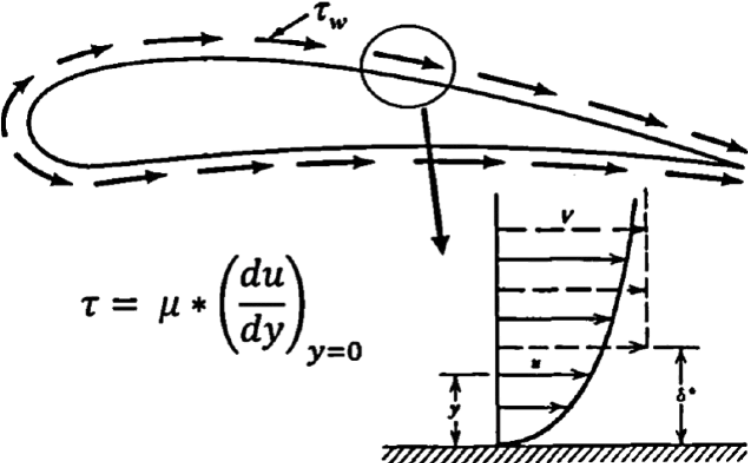
This implies a skin friction coefficient of $$ C_f \equiv \frac{\tau_w}{\tfrac12\rho U^2}\ \sim\ \frac{\left(\frac{\mu U}{L}\right)\mathrm{Re}^{1/2}}{\tfrac12\rho U^2} \ =\ \frac{2}{\sqrt{\mathrm{Re}}} $$ The skin friction coefficient is an important dimensionless parameter in boundary-layer flows. It specifies the fraction of the local dynamic pressure, $\tfrac12\rho U^2$, that is felt as shear stress on the surface. For laminar boundary layers, skin friction coefficient provides the correct order of magnitude and parametric dependence on Reynolds number. However, the numerical factor differs for different laminar boundary-layer flows.