Consider the advection–diffusion equation, which describes how a function \(f(t,x)\) evolves in time and space. Here an arbitrary spatial distribution of a quantity $f$ is carried downstream with a constant velocity $U$, as the profile also changes its shape due to diffusion. The question to be answered is: Given the distribution of $f$ at $t = t_1$, what is its distribution at a later time $t_2 = t_1 + \Delta t$? Or, given $f(t_1, x)$, what is $f(t_2, x)$? To predict that, we need to derive an equation for the evolution of $f$

We start by identifying a specific region of space as our control volume. A control volume has a specific shape, location, and well-defined boundaries, the control surface. In our case, the control volume is a region of length $\Delta x$, and the control surface consists of the two end points

The one-dimensional advection–diffusion equation $$ \underbrace{\frac{\partial \overbrace{f(t,x)}^{\text{conserved quantity}}}{\partial \overbrace{t}^{\text{time}}}}_{\text{local rate of change of }f} \;+\; \underbrace{\overbrace{U}^{\text{constant velocity}} \frac{\partial f}{\partial \overbrace{x}^{\text{space coordinate}}}}_{\text{advection: carried downstream at speed }U} \;=\; \underbrace{\overbrace{D}^{\text{diffusion coefficient}} \frac{\partial^2 f}{\partial x^2}}_{\text{diffusion: spreading set by }D} $$ 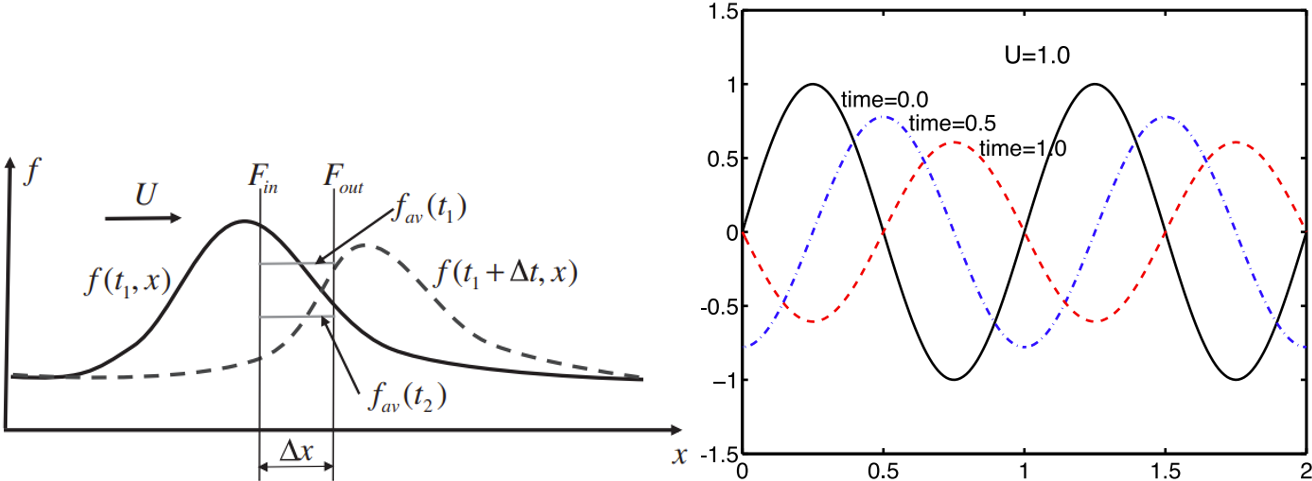This equation can be solved analytically

\[ f(t, x) = e^{-Dk^2t} \sin \big(2\pi k(x - Ut)\big) \] A sine wave will move with a velocity $U$ and decay with time at a rate determined by the diffusion coefficient $D$ and the wave number squared. If the diffusivity is zero, the initial $f$ profile simply moves with the constant velocity $U$