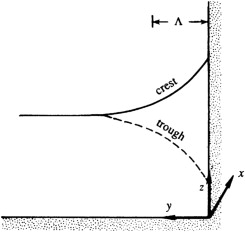
Kelvin Wave
If the left wall is moved away to infinity, what remains is a gravity wave
trapped to the coast. Such coastally-trapped long gravity waves, in which
the transverse velocity \( v = 0 \) everywhere, are called Kelvin waves