Internal Waves

Internal gravity waves unaffected by the Coriolis acceleration are not isotropic; the direction of propagation with respect to the vertical determines their frequency. Their frequency satisfies the inequality $\omega \leq N$, where $\omega$ is the wave (angular) frequency, $N$ is the buoyancy frequency. Their phase-velocity vector $\mathbf{c}$ and the group-velocity vector $\mathbf{c}_g$ are perpendicular and have oppositely directed vertical components

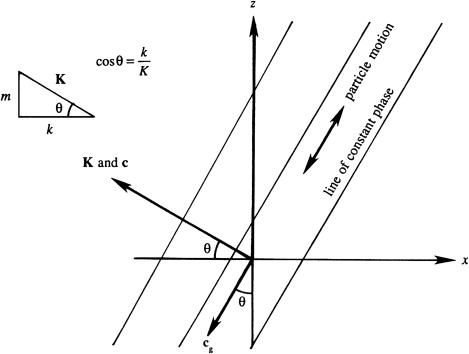
The dispersion relation for internal gravity waves and can be written as \[ \omega = N \cos \theta \] where $\theta = \tan^{-1}(m/k)$ is the angle between the phase velocity vector $\mathbf{c}$ (and therefore $\mathbf{c}$) and the horizontal direction. The frequency of an internal wave in a stratified fluid depends only on the direction of the wave number vector and not on its magnitude. The wave frequency lies in the range $0 < \omega < N$, and this indicates that $N$ is the maximum possible frequency of internal waves in a stratified fluid.

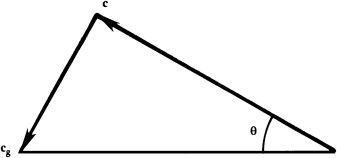
Orientation of phase and group velocity for internal waves. The vertical components of the phase and group velocities are equal and opposite.

Internal waves are ubiquitous in the atmosphere and the ocean. In the lower atmosphere turbulent motions dominate, so that internal wave activity represents a minor component of the motion. In contrast, the stratosphere contains a great deal of internal wave activity, and very little convective motion, because of its stable density distribution. Internal waves generally propagate upward from the lower atmosphere, where they are generated. ◀ ▶